题目内容
14.如图是一座桥的截面图,桥的路面由三段曲线构成,曲线AB和曲线DE分别是顶点在路面A、E的抛物线的一部分,曲线BCD是圆弧,已知它们在接点B、D处的切线相同,若桥的最高点C到水平面的距离H=6米,圆弧的弓高h=1米,圆弧所对的弦长BD=10米.
(1)求弧$\widehat{BCD}$所在圆的半径;
(2)求桥底AE的长.
分析 (1)由r2=52+(r-1)2,即可求得r,即可求得弧$\widehat{BCD}$所在圆的半径;
(2)建立直角坐标系,由题意设$\widehat{BCD}$所在圆的方程,列方程组,即可求得圆的方程,曲线AB所在抛物线的方程为:y=a(x-m)2,求导,根据导数的几何意义,即可求得m的值,求得A和E点坐标,即可求得桥底AE的长为58米.
解答 解:(1)设弧$\widehat{BCD}$所在圆的半径为r(r>0),由题意得r2=52+(r-1)2,则r=13,
即弧$\widehat{BCD}$所在圆的半径为13米. …(4分)
(2)以线段AE所在直线为x轴,线段AE的中垂线为y轴,建立如图的平面直角坐标系.∵H=6米,BD=10米,弓高h=1米,
∴B(-5,5),D(5,5),C(0,6),设$\widehat{BCD}$所在圆的方程为x2+(y-b)2=r2,(r>0),
则$\left\{\begin{array}{l}{(6-b)^2}={r^2}\\{5^2}+{(5-b)^2}={r^2}\end{array}\right.$,$\left\{\begin{array}{l}{b=-7}\\{r=13}\end{array}\right.$,
∴弧$\widehat{BCD}$的方程为x2+(y+7)2=169(5≤y≤6)…6分
设曲线AB所在抛物线的方程为:y=a(x-m)2,…(8分)
由点B(-5,5),在曲线AB上
∴5=a(5+m)2,?…(10分)
又弧$\widehat{BCD}$与曲线段AB在接点B处的切线相同,且弧$\widehat{BCD}$在点B处的切线的斜率为$\frac{5}{12}$,
由y=a(x-m)2,y′=2a(x-m),2a(-5-m)=$\frac{5}{12}$,
2a(5+m)=-$\frac{5}{12}$,…(12分)
由??得m=-29,A(-29,0),E(29,0)
∴桥底AE的长为58米; …(13分)
答:(1)弧$\widehat{BCD}$所在圆的半径为13米;
(2)桥底AE的长58米. (答和单位各1分) …(14分)
点评 本题考查圆方程的求法,抛物线的性质,导数的几何意义,考查计算能力,属于中档题.

| A. | $±\frac{{\sqrt{3}}}{3}$ | B. | ±1 | C. | $±\sqrt{3}$ | D. | ±2 |
| A. | (-1,1) | B. | (-1,0) | C. | (0,1) | D. | (-∞,1) |
| 月平均气温x(℃) | 3 | 8 | 12 | 17 |
| 月销售量y(件) | 24 | 34 | 44 | 54 |
| A. | 46 | B. | 50 | C. | 54 | D. | 59 |
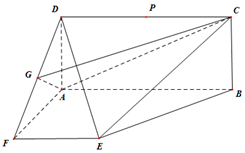 已知矩形ABCD与直角梯形ABEF,∠DAF=∠FAB=90°,点G为DF的中点,AF=EF=$\frac{1}{2}AB=\sqrt{3}$,P在线段CD上运动.
已知矩形ABCD与直角梯形ABEF,∠DAF=∠FAB=90°,点G为DF的中点,AF=EF=$\frac{1}{2}AB=\sqrt{3}$,P在线段CD上运动.