题目内容
4.已知非零向量$\overrightarrow{a}$、$\overrightarrow{b}$满足|$\overrightarrow{a}$-$\overrightarrow{b}$|=|$\overrightarrow{a}$+2$\overrightarrow{b}$|,且$\overrightarrow{a}$与$\overrightarrow{b}$的夹角的余弦值为-$\frac{1}{4}$,则$\frac{|\overrightarrow{a}|}{|\overrightarrow{b}|}$=2.分析 把已知向量等式两边平方,展开数量积公式化简得答案.
解答 解:由|$\overrightarrow{a}$-$\overrightarrow{b}$|=|$\overrightarrow{a}$+2$\overrightarrow{b}$|,得$(\overrightarrow{a}-\overrightarrow{b})^{2}=(\overrightarrow{a}+2\overrightarrow{b})^{2}$,
即$2\overrightarrow{a}•\overrightarrow{b}=-|\overrightarrow{b}{|}^{2}$,
∴$2|\overrightarrow{a}||\overrightarrow{b}|cos<\overrightarrow{a},\overrightarrow{b}>=-|\overrightarrow{b}{|}^{2}$,
∴$\frac{1}{2}|\overrightarrow{a}||\overrightarrow{b}|=|\overrightarrow{b}{|}^{2}$,
得$\frac{|\overrightarrow{a}|}{|\overrightarrow{b}|}=2$.
故答案为:2.
点评 本题考查平面向量的数量积运算,考查数学转化思想方法,是中档题.

练习册系列答案
相关题目
9.已知A(1,-2),B(4,2),则与$\overrightarrow{AB}$反方向的单位向量为( )
| A. | (-$\frac{3}{5}$,$\frac{4}{5}$) | B. | ($\frac{3}{5}$,-$\frac{4}{5}$) | C. | (-$\frac{3}{5}$,-$\frac{4}{5}$) | D. | ($\frac{3}{5}$,$\frac{4}{5}$) |
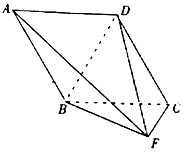 如图,平面ABCD⊥平面BCF,四边形ABCD是菱形,∠BCF=90°.
如图,平面ABCD⊥平面BCF,四边形ABCD是菱形,∠BCF=90°.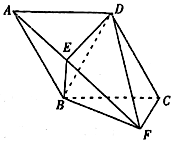 如图,平面ABCD⊥平面BCF,四边形ABCD是菱形,∠BCF=90°.
如图,平面ABCD⊥平面BCF,四边形ABCD是菱形,∠BCF=90°.