题目内容
2.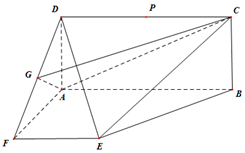 已知矩形ABCD与直角梯形ABEF,∠DAF=∠FAB=90°,点G为DF的中点,AF=EF=$\frac{1}{2}AB=\sqrt{3}$,P在线段CD上运动.
已知矩形ABCD与直角梯形ABEF,∠DAF=∠FAB=90°,点G为DF的中点,AF=EF=$\frac{1}{2}AB=\sqrt{3}$,P在线段CD上运动.(1)证明:BF∥平面GAC;
(2)当P运动到CD的中点位置时,PG与PB长度之和最小,求二面角P-CE-B的余弦值.
分析 (1)连接BD交AC于M,连MG,M为BD的中点,证明GM∥BF,即可证明BF∥平面GAC.
(2)延迟AD至N,使DN=DG,连PN,PG,说明当P、B、N三点共线时,PG与PB长度之和最小,AD,AB,AF两两垂直,如图建立空间直角坐标系,求出相关点的坐标,求出平面PCE的一个法向量,平面BCE的一个法向量,利用空间向量的数量积求解二面角P-CE-B的余弦值.
解答 解:(1)连接BD交AC于M,连MG,M为BD的中点.…(2分)
∴MG为△BFD的中位线,
∴GM∥BF,而BF?平面GAC,MG?平面GAC,
∴BF∥平面GAC.…(5分)
(2)延迟AD至N,使DN=DG,连PN,PG,则△PDG≌△PDN,∴PG=PN
当P、B、N三点共线时,PG与PB长度之和最小,即PG与PB长度之和最小
∵P为CD中点,∴AD=DN.
在△ADF中,AD2+AF2=4DG2=4AD2,∴AD=1…(6分)
AD,AB,AF两两垂直,如图建立空间直角坐标系,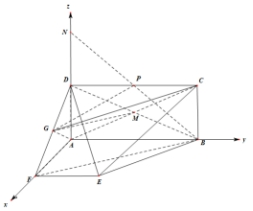
∴D(0,0,1),E($\sqrt{3}$,$\sqrt{3}$,0),B(0,2$\sqrt{3}$,0),C(0,2$\sqrt{3}$,1),
∴$\overrightarrow{CE}$=($\sqrt{3}$,-$\sqrt{3}$,-1),$\overrightarrow{BC}$=(0,0,1),$\overrightarrow{DC}$=(0,2$\sqrt{3}$,0)…(7分)
设$\overrightarrow{n}$=(x,y,z)为平面PCE的一个法向量,
∴$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{CE}=0}\\{\overrightarrow{n}•\overrightarrow{DC}=0}\end{array}\right.$即$\left\{\begin{array}{l}{\sqrt{3}x-\sqrt{3}y-z=0}\\{2\sqrt{3}y=0}\end{array}\right.$,
令x=1,y=0,z=$\sqrt{3}$,$\overrightarrow{n}=(1,0,\sqrt{3})$.
同理可得平面BCE的一个法向量$\overrightarrow{m}$=(1,1,0),…(10分)
设二面角P-CE-B的大小为θ,θ为钝角,
∴cosθ=-$\frac{|\overrightarrow{m}•\overrightarrow{n}|}{|\overrightarrow{\overrightarrow{m}}||\overrightarrow{n}|}$=$-\frac{\sqrt{2}}{4}$,
∴求二面角P-CE-B的余弦值:-$\frac{\sqrt{2}}{4}$…(12分)
点评 本题考查二面角的求法,直线与平面平行的判定定理的应用,考查空间想象能力以及计算能力.

| A. | 3+4i | B. | 3-4i | C. | $\frac{3}{5}$+$\frac{4}{5}$i | D. | $\frac{3}{5}$-$\frac{4}{5}$i |
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)若bn=an+2${\;}^{{a}_{n}}$,求数列{bn}的前n项和Tn.
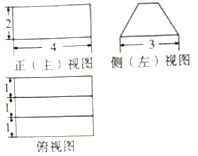
| A. | $\frac{{32+8\sqrt{3}}}{3}$ | B. | 16 | C. | 12 | D. | $32+8\sqrt{3}$ |
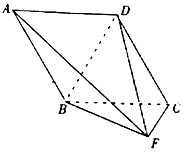 如图,平面ABCD⊥平面BCF,四边形ABCD是菱形,∠BCF=90°.
如图,平面ABCD⊥平面BCF,四边形ABCD是菱形,∠BCF=90°.