题目内容
13.某商场为了了解太阳镜的月销售量y(件)与月平均气温x(℃)之间的关系,随机统计了某4个月的月销售量与当月平均气温,其数据如表:由表中数据算出线性回归方程$\stackrel{∧}{y}$=bx+a中的b=2,气象部门预测下个月的平均气温约为20℃据此估计该商场下个月太阳镜销售量约为( )件.| 月平均气温x(℃) | 3 | 8 | 12 | 17 |
| 月销售量y(件) | 24 | 34 | 44 | 54 |
| A. | 46 | B. | 50 | C. | 54 | D. | 59 |
分析 利用样本中心求出a,得到回归直线方程,然后求解气温约为20℃太阳镜销售量.
解答 解:$\overline{x}$=$\frac{3+8+12+17}{4}$=10,
$\overline{y}$=$\frac{24+34+44+54}{4}$=39.
回归直线方程经过样本中心,所以39=2×10+a,解得a=19.
回归直线方程为:$\stackrel{∧}{y}$=2x+19,
下个月的平均气温约为20℃据此估计该商场下个月太阳镜销售量为:2×20+19=59.
故选:D.
点评 本题考查回归直线方程的求法与应用,是基础题.

练习册系列答案
相关题目
4.某地区2007年至2013年农村居民家庭人均纯收入y(单位:千元)的数据如表:
y关于t的线性回归方程为$\stackrel{∧}{y}$=0.5t+2.3,则a的值为4.8.
| 年份 | 2007 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 |
| 年份代号t | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 人均纯收入y | 2.9 | 3.3 | 3.6 | 4.4 | a | 5.2 | 5.9 |
1.一个空间几何体的三视图及部分数据如下图所示,则该几何体的体积是( )
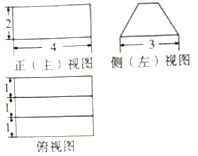

| A. | $\frac{{32+8\sqrt{3}}}{3}$ | B. | 16 | C. | 12 | D. | $32+8\sqrt{3}$ |
18.曲线C1:ρsinθ-2=0,曲线C2:ρ-4cosθ=0,则曲线C1、C2的位置关系是( )
| A. | 相交 | B. | 相切 | C. | 重合 | D. | 相离 |
2.f(x)=alnx+x2-b(x-1)-1,若对$?x∈[\frac{1}{e},+∞)$,f(x)≥0恒成立,则实数a的取值范围是( )
| A. | $a≤{e}+\frac{1}{e}-2$ | B. | a<2 | C. | $\frac{2}{e}≤a<2$ | D. | $a≤\frac{2}{e}$ |
