题目内容
9.已知sinθ=$\frac{1}{3}$,θ∈(0,$\frac{π}{2}$),则tan2θ=$\frac{4\sqrt{2}}{7}$.分析 由已知利用同角三角函数基本关系式可求cosθ,tanθ,进而根据二倍角的正切函数公式即可计算得解.
解答 解:∵sinθ=$\frac{1}{3}$,θ∈(0,$\frac{π}{2}$),
∴cosθ=$\sqrt{1-si{n}^{2}θ}$=$\frac{2\sqrt{2}}{3}$,tan$θ=\frac{sinθ}{cosθ}$=$\frac{\sqrt{2}}{4}$,
∴tan2θ=$\frac{2tanθ}{1-ta{n}^{2}θ}$=$\frac{2×\frac{\sqrt{2}}{4}}{1-(\frac{\sqrt{2}}{4})^{2}}$=$\frac{4\sqrt{2}}{7}$.
故答案为:$\frac{4\sqrt{2}}{7}$.
点评 本题主要考查了同角三角函数基本关系式,二倍角的正切函数公式在三角函数化简求值中的应用,考查了转化思想,属于基础题.

练习册系列答案
相关题目
20.已知集合A={x|2x>1},B={x|x2-5x+6<0},则∁AB( )
| A. | (2,3) | B. | (-∞,2]∪[3,+∞) | C. | (0,2]∪[3,+∞) | D. | [3,+∞) |
17.已知公差不为零的等差数列{an}中,a2=4,且a1,a3,a9成等比数列.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)若bn=an+2${\;}^{{a}_{n}}$,求数列{bn}的前n项和Tn.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)若bn=an+2${\;}^{{a}_{n}}$,求数列{bn}的前n项和Tn.
4.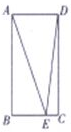 在如图所示的矩形ABCD中,AB=4,AD=2,E为线段BC上的点,则$\overrightarrow{AE}•\overrightarrow{DE}$的最小值为( )
在如图所示的矩形ABCD中,AB=4,AD=2,E为线段BC上的点,则$\overrightarrow{AE}•\overrightarrow{DE}$的最小值为( )
 在如图所示的矩形ABCD中,AB=4,AD=2,E为线段BC上的点,则$\overrightarrow{AE}•\overrightarrow{DE}$的最小值为( )
在如图所示的矩形ABCD中,AB=4,AD=2,E为线段BC上的点,则$\overrightarrow{AE}•\overrightarrow{DE}$的最小值为( )| A. | 12 | B. | 15 | C. | 17 | D. | 16 |
1.函数$f(x)=cos(2x-\frac{2π}{3})+4{cos^2}x-2-\frac{3}{3x-π}(x∈[-\frac{11π}{12},\frac{19π}{12}])$所有零点之和为( )
| A. | $\frac{2π}{3}$ | B. | $\frac{4π}{3}$ | C. | 2π | D. | $\frac{8π}{3}$ |
18.已知a>2,函数f(x)=$\left\{\begin{array}{l}{log_a}({x+1})+x-2,x>0\\ x+4-{(\frac{1}{a})^{x+1}}\begin{array}{l}{\;}{x≤0}\end{array}\end{array}$若函数f(x)有两个零点x1,x2,则( )
| A. | ?a>2,x1-x2=0 | B. | ?a>2,x1-x2=1 | C. | ?a>2,|x1-x2|=2 | D. | ?a>2,|x1-x2|=3 |
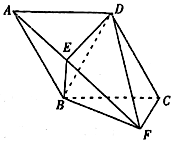 如图,平面ABCD⊥平面BCF,四边形ABCD是菱形,∠BCF=90°.
如图,平面ABCD⊥平面BCF,四边形ABCD是菱形,∠BCF=90°.