题目内容
已知函数f(x)是偶函数,当x≥0时,f(x)=x+1.设函数g(x)=f(t-x)-f(x)的零点为x0,且x0∈[1,2],则非零实数t的取值范围是 .
考点:函数零点的判定定理,函数奇偶性的性质
专题:计算题,函数的性质及应用
分析:由f(x)=x+1在[0,+∞)上单调,函数f(x)是偶函数,且t≠0,函数g(x)=f(t-x)-f(x)的零点为x0,且x0∈[1,2],则t-x=x.
解答:
解:∵f(x)=x+1在[0,+∞)上单调,
又∵函数f(x)是偶函数,且t≠0,
又∵函数g(x)=f(t-x)-f(x)的零点为x0,且x0∈[1,2],
∴t-x与x都在[1,2],
∴t-x=x,
∴t=2x,
∴t∈[2,4].
故答案为:[2,4].
又∵函数f(x)是偶函数,且t≠0,
又∵函数g(x)=f(t-x)-f(x)的零点为x0,且x0∈[1,2],
∴t-x与x都在[1,2],
∴t-x=x,
∴t=2x,
∴t∈[2,4].
故答案为:[2,4].
点评:本题考查了函数的零点的判断,属于基础题.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
若a,b,c∈R,且a>b,则下列结论一定成立的是( )
| A、a>bc | ||||
B、
| ||||
| C、a-c>b-c | ||||
| D、a2>b2 |
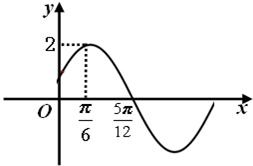 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<