题目内容
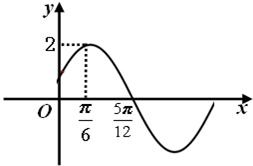 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<| π |
| 2 |
(1)求函数f(x)的解析式;
(2)求f(x)单调减区间;
(3)求函数f(x)的最大值,并且求使f(x)取得最大值时的x的取值范围.
考点:由y=Asin(ωx+φ)的部分图象确定其解析式,正弦函数的单调性
专题:三角函数的图像与性质
分析:(1)首先,根据图象,得到A=2,然后,根据周期,得到ω的值,最后,确定φ=
;
(2)直接结合正弦函数的单调区间进行求解即可;
(3)根据正弦函数的最大值取值情形进行求解.
| π |
| 6 |
(2)直接结合正弦函数的单调区间进行求解即可;
(3)根据正弦函数的最大值取值情形进行求解.
解答:
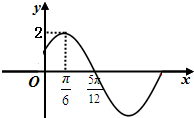 18、解:(1)由图象知A=2,
18、解:(1)由图象知A=2,
f(x)的最小正周期T=4×(
-
)=π,故ω=
=2 …(3分)
将点(
,2)代入f(x),得解析式sin(
+φ)=1,又|φ|<
,
∴φ=
…(5分)
故函数f(x)的解析式为f(x)=2sin(2x+
).…(6分)
(2)令
+2kπ≤2x+
≤2kπ+
,k∈Z,
∴
+kπ≤x≤
+kπ,
∴f(x)单调减区间[
+kπ,
+kπ],(k∈Z) …(10分)
(3)当sin(2x+
)=1时,f(x)有最大值,
f(x)的最大值是2,此时x的取值范围是:{x|x=
+kπ,k∈Z}.
 18、解:(1)由图象知A=2,
18、解:(1)由图象知A=2,f(x)的最小正周期T=4×(
| 5π |
| 12 |
| π |
| 6 |
| 2π |
| T |
将点(
| π |
| 6 |
| π |
| 3 |
| π |
| 2 |
∴φ=
| π |
| 6 |
故函数f(x)的解析式为f(x)=2sin(2x+
| π |
| 6 |
(2)令
| π |
| 2 |
| π |
| 6 |
| 3π |
| 2 |
∴
| π |
| 6 |
| π |
| 3 |
∴f(x)单调减区间[
| π |
| 6 |
| π |
| 3 |
(3)当sin(2x+
| π |
| 6 |
f(x)的最大值是2,此时x的取值范围是:{x|x=
| π |
| 6 |
点评:本题重点考查了三角函数的图象与性质、三角公式及其运用等知识,属于中档题.

练习册系列答案
相关题目
已知四面体的各条棱长均为2,则它的表面积是( )
A、
| ||
B、2
| ||
C、4
| ||
D、8
|
直线3x-4y+6=0与圆(x-2)2+(y-3)2=4的位置关系是( )
| A、直线与圆相交且过圆心 |
| B、直线与圆相交但不过圆心 |
| C、相切 |
| D、相离 |
 如图,抛物线C1:y2=4x,圆C2:(x-1)2+y2=1,过抛物线焦点的直线l
如图,抛物线C1:y2=4x,圆C2:(x-1)2+y2=1,过抛物线焦点的直线l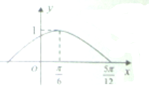 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,-
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,-