题目内容
D(x)=
,则给出下列结论
①函数D(x)的定义域为{x|x≠0};
②函数D(x)的值域[0,1];
③函数D(x)是偶函数;
④函数D(x)不是单调函数.
⑤对任意的x∈R,都存在T0∈R,使得D(x+T0)=D(x).
其中的正确的结论是 (写出所有正确结论的序号).
|
①函数D(x)的定义域为{x|x≠0};
②函数D(x)的值域[0,1];
③函数D(x)是偶函数;
④函数D(x)不是单调函数.
⑤对任意的x∈R,都存在T0∈R,使得D(x+T0)=D(x).
其中的正确的结论是
考点:分段函数的应用
专题:阅读型,函数的性质及应用
分析:由函数定义域的概念易知结论①不正确;由函数值域的概念易知结论②不正确;
由偶函数定义可证明结论③正确;由函数单调性定义,易知④结论正确;
由分段函数的定义和有理数与无理数的概念,可证明结论⑤正确.
由偶函数定义可证明结论③正确;由函数单调性定义,易知④结论正确;
由分段函数的定义和有理数与无理数的概念,可证明结论⑤正确.
解答:
解:由于D(x)=
,
则①函数的定义域为R,故①错;
②函数D(x)的值域是{0,1},故②错;
③由于D(-x)=
=D(x),则D(x)是偶函数,故③正确;
④由于D(
)=0,D(2)=1,D(
)=0,显然函数D(x)不是单调函数,故④正确;
⑤当x为有理数时,D(x)=1,要使D(x+T0)=D(x)=1,则存在T0∈Q,使得x+T0为有理数成立;
当x为无理数时,D(x)=0,要使D(x+T0)=D(x)=0,则存在T0∈R,使得x+T0为无理数成立.
对任意的x∈R,都存在T0∈R,使得D(x+T0)=D(x).故⑤正确.
故答案为:③④⑤
|
则①函数的定义域为R,故①错;
②函数D(x)的值域是{0,1},故②错;
③由于D(-x)=
|
④由于D(
| 2 |
| 5 |
⑤当x为有理数时,D(x)=1,要使D(x+T0)=D(x)=1,则存在T0∈Q,使得x+T0为有理数成立;
当x为无理数时,D(x)=0,要使D(x+T0)=D(x)=0,则存在T0∈R,使得x+T0为无理数成立.
对任意的x∈R,都存在T0∈R,使得D(x+T0)=D(x).故⑤正确.
故答案为:③④⑤
点评:本题考查分段函数及运用,考查函数的性质和运用,考查函数的单调性、奇偶性、值域等性质,考查推理能力,属于中档题.

练习册系列答案
 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案
相关题目
直线3x-4y+6=0与圆(x-2)2+(y-3)2=4的位置关系是( )
| A、直线与圆相交且过圆心 |
| B、直线与圆相交但不过圆心 |
| C、相切 |
| D、相离 |
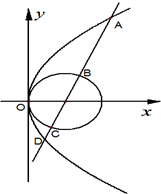 如图,抛物线C1:y2=4x,圆C2:(x-1)2+y2=1,过抛物线焦点的直线l
如图,抛物线C1:y2=4x,圆C2:(x-1)2+y2=1,过抛物线焦点的直线l