题目内容
9.若函数f(x)=x2+px+3在(-∞,1]上单调递减,则p的取值范围是(-∞,-2].分析 求出二次函数的对称轴方程,由二次函数的减区间,可得在对称轴的右边,解不等式即可得到所求范围.
解答 解:函数f(x)=x2+px+3在的对称轴为x=-$\frac{p}{2}$,
在(-∞,-$\frac{p}{2}$]递减,
由题意可得-$\frac{p}{2}$≥1,
解得p≤-2.
故答案为:(-∞,-2].
点评 本题考查二次函数的性质:单调性,考查运算能力,属于基础题.

练习册系列答案
相关题目
19.等差数列{an}中,a4=4,a3+a8=5,则a7=( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
20.$\root{3}{-27}$等于( )
| A. | 3 | B. | -3 | C. | ±3 | D. | -27 |
17.已知数列{an}是等差数列,且a2+a3+a10+a11=48,则a5+a8等于( )
| A. | 12 | B. | 18 | C. | 24 | D. | 30 |
4.已知奇函数f(x)在(0,+∞)上是增函数,且f(2)=0,则f(x)>0的解集为( )
| A. | (0,2) | B. | (-2,0) | C. | (-2,0)∪(2,+∞) | D. | (-2,2) |
14.下列表示正确的是( )
| A. | ∅∈{0} | B. | {3}∈{1,3} | C. | 0⊆{0,1} | D. | ∅⊆{2} |
1.在△ABC中,a,b,c分别是角A,B,C的对边,且A=60°,a=7,c=5,则△ABC的面积等于( )
| A. | $\frac{{15\sqrt{3}}}{4}$ | B. | $\frac{15}{4}$ | C. | $10\sqrt{3}$ | D. | 10 |
19.一个几何体的三视图如图,则该几何体的体积为( )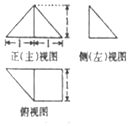

| A. | 2 | B. | $\frac{3}{2}$ | C. | 1 | D. | $\frac{1}{2}$ |