题目内容
若(cosa)2+2msina-2m-2<0对a∈R恒成立,则实数m的取值范围 .
考点:函数恒成立问题
专题:函数的性质及应用
分析:将不等式进行转化,利用换元法将函数转化为一元二次函数,根据一元二次函数的性质建立不等式关系即可得到结论.
解答:
解:不等式等价为1-sin2a+2msina-2m-2<0对一切a∈R恒成立,
即sin2a-2msina+2m+1>0恒成立,
设t=sina,则-1≤t≤1,
则不等式等价为t2-2mt+2m+1>0,在-1≤t≤1上恒成立,
设f(t)=t2-2mt+2m+1,-1≤t≤1,
对称性t=m,
若m≤-1,则函数f(t)在[-1,1]上为增函数,
则满足f(-1)=1+2m+2m+1=4m+2>0,
即m>-
,此时不成立,
若-1<m<1,
则满足f(m)=m2-2m2+2m+1>0,
即m2-2m-1<0,
解得1-
<m<1+
,
此时1-
<m<1,
若m≥1,则函数f(t)在[-1,1]上为减函数,
则满足f(1)=1-2m+2m+1=2>0,恒成立,
此时m≥1,
综上m>1-
,
故答案为:(1-
,+∞)
即sin2a-2msina+2m+1>0恒成立,
设t=sina,则-1≤t≤1,
则不等式等价为t2-2mt+2m+1>0,在-1≤t≤1上恒成立,
设f(t)=t2-2mt+2m+1,-1≤t≤1,
对称性t=m,
若m≤-1,则函数f(t)在[-1,1]上为增函数,
则满足f(-1)=1+2m+2m+1=4m+2>0,
即m>-
| 1 |
| 2 |
若-1<m<1,
则满足f(m)=m2-2m2+2m+1>0,
即m2-2m-1<0,
解得1-
| 2 |
| 2 |
此时1-
| 2 |
若m≥1,则函数f(t)在[-1,1]上为减函数,
则满足f(1)=1-2m+2m+1=2>0,恒成立,
此时m≥1,
综上m>1-
| 2 |
故答案为:(1-
| 2 |
点评:此题考查函数的恒成立问题,利用换元法结合一元二次不等式和一元二次函数的性质是解决本题的关键.

练习册系列答案
 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案
相关题目
设f(n)>0(n∈N*),f(2)=4,并且对于任意n2,n2∈N*,有f(n1+n2)=f(n1)•f(n2)成立,猜想f(n)的表达式为( )
| A、f(n)=n2 |
| B、f(n)=2n |
| C、f(n)=2n+1 |
| D、f(n)=2n |
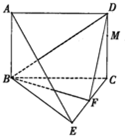 如图,平面ABCD⊥平面BCE,四边形ABCD为矩形,BC=CE,点F为CE的中点.
如图,平面ABCD⊥平面BCE,四边形ABCD为矩形,BC=CE,点F为CE的中点.