题目内容
已知|
|=2，（
+
）⊥（
-
），求|
|
| a |
| a |
| b |
| a |
| b |
| b |
考点：平面向量数量积的运算
专题：计算题,平面向量及应用
分析：运用向量垂直的条件，即为数量积为0，运用平方差化简，再由向量的平方即为模的平方，即可得到所求值．
解答：
解：由于（
+
）⊥（
-
），
则（
+
）•（
-
）=0，
即有
2-
2=0，
即|
|=|
|=2．
| a |
| b |
| a |
| b |
则（
| a |
| b |
| a |
| b |
即有
| a |
| b |
即|
| b |
| a |
点评：本题考查向量垂直的条件，考查运算能力，属于基础题．
练习册系列答案
相关题目
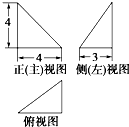
某四面体的三视图如图所示，三个三角形均为直角三角形，则该四面体的表面积是（ ）
| A、8 | ||
B、22+2
| ||
C、18+6
| ||
D、24+6
|