题目内容
设f（n）＞0（n∈N*），f（2）=4，并且对于任意n2，n2∈N*，有f（n1+n2）=f（n1）•f（n2）成立，猜想f（n）的表达式为（ ）
| A、f（n）=n2 |
| B、f（n）=2n |
| C、f（n）=2n+1 |
| D、f（n）=2n |
考点：归纳推理
专题：计算题,函数的性质及应用
分析：由f（n1+n2）=f（n1）•f（n2）知，f（n）可以为指数型函数，从而得到答案．
解答：
解：由f（n1+n2）=f（n1）•f（n2），
结合指数运算律：as×at=as+t知，
f（n）可以为指数型函数，
故排除A，B；
而再由f（2）=4知，
f（n）=2n，
故选D．
结合指数运算律：as×at=as+t知，
f（n）可以为指数型函数，
故排除A，B；
而再由f（2）=4知，
f（n）=2n，
故选D．
点评：本题考查了指数函数的应用，属于基础题．
练习册系列答案
阅读快车系列答案
相关题目
f（x）是定义在R上的偶函数，且在（0，+∞）上是减函数，若x2＞x1，x1+x2＞0，则下列说法正确的是（ ）
| A、f（x1）＞f（x2） |
| B、f（x1）=f（x2） |
| C、f（x1）＜f（x2） |
| D、f（x1）和f（x2）的大小关系不能确定 |
已知向量
=
，
=
，且
与
不共线，C为线段AB上距点A较近的一个三等分点，则以
，
为基底，向量
可表示为（ ）
| OA |
| a |
| OB |
| b |
| a |
| b |
| a |
| b |
| OC |
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
某四面体的三视图如图所示，三个三角形均为直角三角形，则该四面体的表面积是（ ）
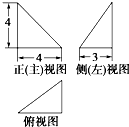
| A、8 | ||
B、22+2
| ||
C、18+6
| ||
D、24+6
|