题目内容
已知y>x>0,若以x+y,
,λx为三边能构成一个三角形,则λ的取值范围 .
| x2+y2 |
考点:三角形中的几何计算
专题:函数的性质及应用,导数的综合应用
分析:根据构成三角形的条件:两边之和大于第三边可得到,
,对于③容易判断对于任意λ>0都成立.要求λ的取值范围,所以由①得λ<1+
+
,令
=t,t>1,f(t)=1+t+
,通过对f(t)求导容易判断f(t)在(1,+∞)单调递增,所以f(t)>f(1)=2+
,所以便得到λ≤2+
.同样的办法由②可得到λ>1+
-
,令
=t,t>1,g(t)=1+t-
,并通过求导可判断出g(t)在(1,+∞)上单调递增,并且可将g(t)变成:g(t)=
,所以当t趋向正无穷时,g(t)趋向1,所以便有t≥1,综上便得到1≤t≤2+
.
|
| y |
| x |
1+(
|
| y |
| x |
| 1+t2 |
| 2 |
| 2 |
| y |
| x |
1+(
|
| y |
| x |
| 1+t2 |
| 2 | ||||||
1+
|
| 2 |
解答:
解:根据已知条件得:
;
∵y>x>0,∴x+y=
>
;
λ>0,∴x+y+λx>
对于任意y>x>0,λ>0都成立;
∴(1)由①得,λ<1+
+
,令
=t,t>1,f(t)=1+t+
;
f′(t)=1+
>0;
∴f(t)在(1,+∞)上单调递增;
∴f(t)>f(1)=2+
;
∴λ≤2+
;
(2)由②得,λ>1+
-
,令
=t,t>1,g(t)=1+t-
;
g′(t)=
>0;
∴g(t)在(1,+∞)单调递增;
g(t)=
=
;
∴t趋向正无穷时,g(t)趋向1;
∴g(t)<1;
∴λ≥1;
∴综合(1)(2)得1≤λ≤2+
;
即λ的取值范围为[1,2+
].
故答案为:[1,2+
].
|
∵y>x>0,∴x+y=
| x2+y2+2xy |
| x2+y2 |
λ>0,∴x+y+λx>
| x2+y2 |
∴(1)由①得,λ<1+
| y |
| x |
1+(
|
| y |
| x |
| 1+t2 |
f′(t)=1+
| t | ||
|
∴f(t)在(1,+∞)上单调递增;
∴f(t)>f(1)=2+
| 2 |
∴λ≤2+
| 2 |
(2)由②得,λ>1+
| y |
| x |
1+(
|
| y |
| x |
| 1+t2 |
g′(t)=
| ||
|
∴g(t)在(1,+∞)单调递增;
g(t)=
| 2t | ||
1+t+
|
| 2 | ||||||
1+
|
∴t趋向正无穷时,g(t)趋向1;
∴g(t)<1;
∴λ≥1;
∴综合(1)(2)得1≤λ≤2+
| 2 |
即λ的取值范围为[1,2+
| 2 |
故答案为:[1,2+
| 2 |
点评:考查三角形三边的关系:两边之和大于第三边,这也是三条线段构成三角形的条件,在解题过程中换元的方法,以及根据导数符号判断函数单调性的方法.

练习册系列答案
 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案
相关题目
若函数y=-x2+4x-3的定义域为[0,t],值域为[-3,1],则t的取值范围是( )
| A、(0,4] | ||
B、[
| ||
| C、[2,4] | ||
| D、[2,+∞) |
计算机执行如图的程序语句后,输出的结果是( )


| A、1,3 | B、4,1 |
| C、1,1 | D、4,-2 |
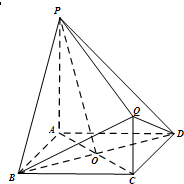 如图,PA,QC都与正方形ABCD所在平面垂直,AB=PA=2QC=2,AC∩BD=O
如图,PA,QC都与正方形ABCD所在平面垂直,AB=PA=2QC=2,AC∩BD=O