题目内容
设关于x函数f(x)=cos2x-4acosx+2a其中0≤x≤
(1)将f(x)的最小值m表示成a的函数m=g(a);
(2)是否存在实数a,使f(x)>0在x∈[0,
]上恒成立?
(3)是否存在实数a,使函数f(x) 在x∈[0,
]上单调递增?若存在,写出所有的a组成的集合;若不存在,说明理由.
| π |
| 2 |
(1)将f(x)的最小值m表示成a的函数m=g(a);
(2)是否存在实数a,使f(x)>0在x∈[0,
| π |
| 2 |
(3)是否存在实数a,使函数f(x) 在x∈[0,
| π |
| 2 |
考点:二倍角的余弦,余弦函数的定义域和值域
专题:综合题,三角函数的求值
分析:(1)换元,利用配方法,再分类讨论,即可求出函数m=g(a);
(2)f(x)>0恒成立?g(a)>0,结合g(a)的最大值,即可得出结论;
(3)由题意,y=2(t-a)2-2a2+2a-1在[0,1]上单调递减,即可求出所有的a组成的集合.
(2)f(x)>0恒成立?g(a)>0,结合g(a)的最大值,即可得出结论;
(3)由题意,y=2(t-a)2-2a2+2a-1在[0,1]上单调递减,即可求出所有的a组成的集合.
解答:
解:(1)设t=cosx,由0≤x≤
知t∈[0,1]
f(x)=2cos2x-4acosx+2a-1=2(t-a)2-2a2+2a-1.
当a<0时,g(a)=2a-1;
当0≤a≤1时,g(a)=-2a2+2a-1;
当a≥1时,g(a)=1-2a.
所以g(a)=
;
(2)f(x)>0恒成立?g(a)>0,
由于g(a)的最大值为-
,所以g(a)>0无解.
故不存在a,使得f(x)>0恒成立.
(3)因为t=cosx在[0,
]上的减函数,
所以f(x)在[0,
]上递增,只需y=2(t-a)2-2a2+2a-1在[0,1]上单调递减,故a≥1
所以存在a∈[1,+∞),使函数f(x)为增函数.
| π |
| 2 |
f(x)=2cos2x-4acosx+2a-1=2(t-a)2-2a2+2a-1.
当a<0时,g(a)=2a-1;
当0≤a≤1时,g(a)=-2a2+2a-1;
当a≥1时,g(a)=1-2a.
所以g(a)=
|
(2)f(x)>0恒成立?g(a)>0,
由于g(a)的最大值为-
| 1 |
| 2 |
故不存在a,使得f(x)>0恒成立.
(3)因为t=cosx在[0,
| π |
| 2 |
所以f(x)在[0,
| π |
| 2 |
所以存在a∈[1,+∞),使函数f(x)为增函数.
点评:本题考查的是余弦函数的定义域和值域,考查函数的最值与单调性,难度中等.

练习册系列答案
 一课一练课时达标系列答案
一课一练课时达标系列答案
相关题目
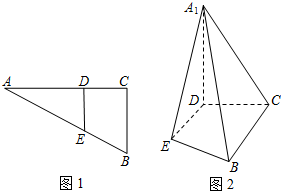 如图1直角△ABC中,两直角边长分别是BC=3,AC=6,D、E分别是AC、AB上的点,且DE∥BC,将△ADE沿DE折起到△A1DE的位置,使A1D⊥CD(如图2)
如图1直角△ABC中,两直角边长分别是BC=3,AC=6,D、E分别是AC、AB上的点,且DE∥BC,将△ADE沿DE折起到△A1DE的位置,使A1D⊥CD(如图2) 如图,在四棱锥P-ABCD中,PD⊥平面ABCD,ABCD是正方形,E为PC的中点.
如图,在四棱锥P-ABCD中,PD⊥平面ABCD,ABCD是正方形,E为PC的中点. 如图,四边形ABCD为平行四边形,四边形ADEF是正方形,且BD⊥平面CDE,H是BE的中点,G是AE,DF的交点.
如图,四边形ABCD为平行四边形,四边形ADEF是正方形,且BD⊥平面CDE,H是BE的中点,G是AE,DF的交点. 如图,在四棱锥V-ABCD中,底面ABCD为正方形,侧面VAD是正三角形,平面VAD⊥底面ABCD.
如图,在四棱锥V-ABCD中,底面ABCD为正方形,侧面VAD是正三角形,平面VAD⊥底面ABCD.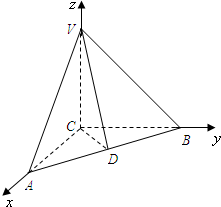 如图,在三棱锥V-ABC中,顶点C在空间直角坐标系的原点处,顶点A、B、V分别在x、y、z轴上,D是AB的中点,且AC=BC=2,∠VDC=θ.
如图,在三棱锥V-ABC中,顶点C在空间直角坐标系的原点处,顶点A、B、V分别在x、y、z轴上,D是AB的中点,且AC=BC=2,∠VDC=θ.