题目内容
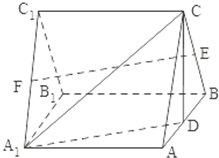 如图,三棱柱ABC-A1B1C1中,侧棱A1A⊥底面ABC,且各棱长均相等.D,E,F分别为棱AB,BC,A1C1的中点.
如图,三棱柱ABC-A1B1C1中,侧棱A1A⊥底面ABC,且各棱长均相等.D,E,F分别为棱AB,BC,A1C1的中点.(1)证明EF∥平面A1CD;
(2)证明平面A1CD⊥平面A1ABB1.
考点:平面与平面垂直的判定,直线与平面平行的判定
专题:证明题,空间位置关系与距离
分析:(1)连接ED,证明四边形A1DEF是平行四边形,可得EF∥A1D.利用线面平行的判定定理,即可证明EF∥平面A1CD;
(2)证明CD⊥面A1ABB1,即可证明平面A1CD⊥平面A1ABB1.
(2)证明CD⊥面A1ABB1,即可证明平面A1CD⊥平面A1ABB1.
解答:
 证明:(1)连接ED,∵ED∥AC,ED=
证明:(1)连接ED,∵ED∥AC,ED=
AC
又∵F为A1C1的中点.
∴A1F∥DE,A1F=DE
∴四边形A1DEF是平行四边形
∴EF∥A1D
又A1D?平面A1CD,EF?平面A1CD
∴EF∥平面A1CD …(4分)
(2)∵A1A⊥平面ABC,
∴A1A⊥CD
∵D是AB的中点,
∴AB⊥CD
∴CD⊥面A1ABB1,
∴平面A1CD⊥平面A1ABB1.…(8分)
 证明:(1)连接ED,∵ED∥AC,ED=
证明:(1)连接ED,∵ED∥AC,ED=| 1 |
| 2 |
又∵F为A1C1的中点.
∴A1F∥DE,A1F=DE
∴四边形A1DEF是平行四边形
∴EF∥A1D
又A1D?平面A1CD,EF?平面A1CD
∴EF∥平面A1CD …(4分)
(2)∵A1A⊥平面ABC,
∴A1A⊥CD
∵D是AB的中点,
∴AB⊥CD
∴CD⊥面A1ABB1,
∴平面A1CD⊥平面A1ABB1.…(8分)
点评:本题考查线面平行,面面垂直,正确运用线面平行,面面垂直的判定定理是关键.

练习册系列答案
相关题目
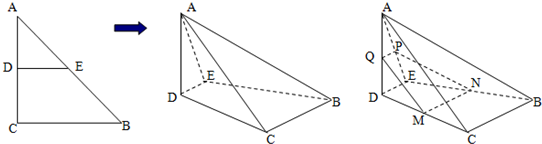
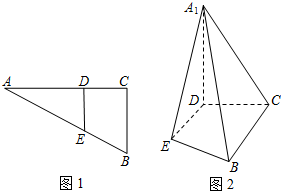 如图1直角△ABC中,两直角边长分别是BC=3,AC=6,D、E分别是AC、AB上的点,且DE∥BC,将△ADE沿DE折起到△A1DE的位置,使A1D⊥CD(如图2)
如图1直角△ABC中,两直角边长分别是BC=3,AC=6,D、E分别是AC、AB上的点,且DE∥BC,将△ADE沿DE折起到△A1DE的位置,使A1D⊥CD(如图2)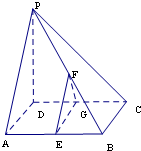 如图,在四棱锥P-ABCD中,PD⊥底面ABCD,底面ABCD为正方形,PD=DC,E,F、G分别是AB,PB,CD的中点.
如图,在四棱锥P-ABCD中,PD⊥底面ABCD,底面ABCD为正方形,PD=DC,E,F、G分别是AB,PB,CD的中点. 已知平行四边形ABCD的对角线相交于点O,G是平行四边形ABCD所在平面外一点,且GA=GC,GB=GD,求证:GO⊥平面ABCD.
已知平行四边形ABCD的对角线相交于点O,G是平行四边形ABCD所在平面外一点,且GA=GC,GB=GD,求证:GO⊥平面ABCD. 如图,在四棱锥P-ABCD中,PD⊥平面ABCD,ABCD是正方形,E为PC的中点.
如图,在四棱锥P-ABCD中,PD⊥平面ABCD,ABCD是正方形,E为PC的中点. 如图,四边形ABCD为平行四边形,四边形ADEF是正方形,且BD⊥平面CDE,H是BE的中点,G是AE,DF的交点.
如图,四边形ABCD为平行四边形,四边形ADEF是正方形,且BD⊥平面CDE,H是BE的中点,G是AE,DF的交点.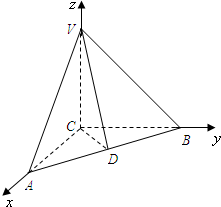 如图,在三棱锥V-ABC中,顶点C在空间直角坐标系的原点处,顶点A、B、V分别在x、y、z轴上,D是AB的中点,且AC=BC=2,∠VDC=θ.
如图,在三棱锥V-ABC中,顶点C在空间直角坐标系的原点处,顶点A、B、V分别在x、y、z轴上,D是AB的中点,且AC=BC=2,∠VDC=θ.