题目内容
设f(x)=ex(ax2+x+1),且曲线y=f(x)在x=1处的切线与x轴平行.
(1)求a的值;
(2)求f(x)的单调区间;
(3)求f(x)在[-3,2]的最小值.
参考公式:(ex)′=ex,(f(x)g(x))′=(f(x))′g(x)+f(x)(g(x))′.
(1)求a的值;
(2)求f(x)的单调区间;
(3)求f(x)在[-3,2]的最小值.
参考公式:(ex)′=ex,(f(x)g(x))′=(f(x))′g(x)+f(x)(g(x))′.
考点:利用导数研究函数的单调性,利用导数求闭区间上函数的最值
专题:导数的概念及应用
分析:(1)先求出函数的导数,再由f′(1)=0,求出a的值即可;(2)先求出导函数,解关于导函数的不等式,进而求出单调区间,(3)找出极值点,求出极值及端点值即可求出最小值.
解答:
解:(1)f′(x)=ex(ax2+x+1+2ax+1),
由条件知,f′(1)=0,
故a+3+2a=0,
∴a=-1.
(2)f(x)=ex(-x2+x+1),
于是f′(x)=ex(-x2-x+2)=-ex(x+2)(x-1),
故当x∈(-∞,-2)和(1,+∞)时,f′(x)<0;
当x∈(-2,1)时,f′(x)>0,
从而f(x)在(-∞,-2),(1,+∞)上单调递减,在(-2,1)上单调递增.
(3)由(2)知,f(x)在(-3,-2)和(1,2)上单调递减,在(-2,1)上单调递增,所以,f(x)在x=-2或2处取得最小值,
f(-2)=-
,f(2)=-e2,
∴f(x)在[-3,2]的最小值是f(2)=-e2.
由条件知,f′(1)=0,
故a+3+2a=0,
∴a=-1.
(2)f(x)=ex(-x2+x+1),
于是f′(x)=ex(-x2-x+2)=-ex(x+2)(x-1),
故当x∈(-∞,-2)和(1,+∞)时,f′(x)<0;
当x∈(-2,1)时,f′(x)>0,
从而f(x)在(-∞,-2),(1,+∞)上单调递减,在(-2,1)上单调递增.
(3)由(2)知,f(x)在(-3,-2)和(1,2)上单调递减,在(-2,1)上单调递增,所以,f(x)在x=-2或2处取得最小值,
f(-2)=-
| 5 |
| e2 |
∴f(x)在[-3,2]的最小值是f(2)=-e2.
点评:本题考察了函数的单调性,求函数闭区间上的最值问题,是一道基础题.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
 如图,在四棱锥P-ABCD中,PD⊥平面ABCD,ABCD是正方形,E为PC的中点.
如图,在四棱锥P-ABCD中,PD⊥平面ABCD,ABCD是正方形,E为PC的中点. 如图,在四棱锥V-ABCD中,底面ABCD为正方形,侧面VAD是正三角形,平面VAD⊥底面ABCD.
如图,在四棱锥V-ABCD中,底面ABCD为正方形,侧面VAD是正三角形,平面VAD⊥底面ABCD.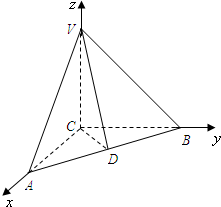 如图,在三棱锥V-ABC中,顶点C在空间直角坐标系的原点处,顶点A、B、V分别在x、y、z轴上,D是AB的中点,且AC=BC=2,∠VDC=θ.
如图,在三棱锥V-ABC中,顶点C在空间直角坐标系的原点处,顶点A、B、V分别在x、y、z轴上,D是AB的中点,且AC=BC=2,∠VDC=θ.