题目内容
已知实数a，b满足|a|＜2，|b|＜2，证明：2|a+b|＜|4+ab|．
考点：不等式的证明
专题：选作题,不等式
分析：证法一，利用综合法；证法二，利用分析法证明．
解答：
证明：证法一：∵|a|＜2，|b|＜2，∴a2＜4，b2＜4，
∴4-a2＞0，4-b2＞0．…（2分）
∴（4-a2）（4-b2）＞0，即16-4a2-4b2+a2b2＞0，…（4分）
∴4a2+4b2＜16+a2b2，
∴4a2+8ab+4b2＜16+8ab+a2b2，…（6分）
即（2a+2b）2＜（4+ab）2，
∴2|a+b|＜|4+ab|．…（8分）
证法二：要证2|a+b|＜|4+ab|，
只需证4a2+4b2+8ab＜16+a2b2+8ab，…（2分）
只需证4a2+4b2＜16+a2b2，
只需证16+a2b2-4a2-4b2＞0，…（4分）
即（4-a2）（4-b2）＞0．…（6分）∵|a|＜2，|b|＜2，∴a2＜4，b2＜4，∴（4-a2）（4-b2）＞0成立．
∴要证明的不等式成立．…（8分）
∴4-a2＞0，4-b2＞0．…（2分）
∴（4-a2）（4-b2）＞0，即16-4a2-4b2+a2b2＞0，…（4分）
∴4a2+4b2＜16+a2b2，
∴4a2+8ab+4b2＜16+8ab+a2b2，…（6分）
即（2a+2b）2＜（4+ab）2，
∴2|a+b|＜|4+ab|．…（8分）
证法二：要证2|a+b|＜|4+ab|，
只需证4a2+4b2+8ab＜16+a2b2+8ab，…（2分）
只需证4a2+4b2＜16+a2b2，
只需证16+a2b2-4a2-4b2＞0，…（4分）
即（4-a2）（4-b2）＞0．…（6分）∵|a|＜2，|b|＜2，∴a2＜4，b2＜4，∴（4-a2）（4-b2）＞0成立．
∴要证明的不等式成立．…（8分）
点评：本题考查不等式的证明，综合法、分析法的应用，考查分析问题解决问题的能力．
练习册系列答案
仁爱英语同步练习册系列答案
学习实践园地系列答案
相关题目
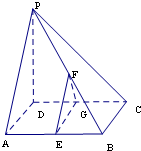如图，在四棱锥P-ABCD中，PD⊥底面ABCD，底面ABCD为正方形，PD=DC，E，F、G分别是AB，PB，CD的中点．
如图，在四棱锥P-ABCD中，PD⊥平面ABCD，ABCD是正方形，E为PC的中点．