题目内容

已知AB=2，∠B=60°，AC=b，若b∈M时△ABC能唯一确定，则集合M=
 
．
考点：余弦定理的应用
专题：计算题,解三角形
分析：利用正弦定理列出关系式，将各自的值代入表示出b，根据C的范围求出sinC的范围，即可确定出b的范围．
解答： 解：∵△ABC中，∠ABC=60°，AC=b，AB=2，
∴由正弦定理
a
sinA
=
b
sinB
=
c
sinC
，得：
2
sinC
=
b
sin60°
，即b=
3
sinC
，
∵0°＜C＜120°，∴0＜sinC≤1，
且b≥2，
则b的取值范围为M=[2，+∞）∪{
3
}．
故答案为：[2，+∞）∪{
3
}．
点评：此题考查了正弦定理，以及正弦函数的定义域与值域，熟练掌握正弦定理是解本题的关键．
练习册系列答案
相关题目
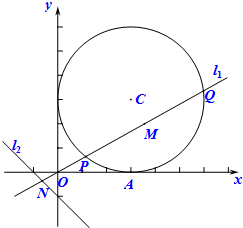已知圆C：（x-3）2+（y-3）2=9，直线l1：y=kx与圆C交于P、Q两个不同的点，M为P、Q的中点．
（Ⅰ）已知A（3，0），若
AP
•
AQ
=0，求实数k的值；
（Ⅱ）求点M的轨迹方程；
（Ⅲ）若直线l1与l2：x+y+1=0的交点为N，求证：|OM|•|ON|为定值．
已知实数a，b满足3a+b=1，则
a+
1
2
+
b+
1
2
的最大值是
 
．
已知函数f（x）=log2（x+1）+log2
1
1-x
．
（1）判断并证明函数f（x）的奇偶性；
（2）若关于x的方程f（x）-m=0在区间[0，1）内仅有一解，求实数m的最小值．
在四棱锥P-ABCD中，AD∥BC，∠ABC=∠APB=90°，
AB
=4
MB
，且PM⊥CD，AB=BC=2PB=2AD．
（1）证明：面PAB⊥面ABCD；
（2）求直线DM与平面PCD所成角的正弦值．
已知单位向量
a
与
b
的夹角是钝角，当t∈R时，|
a
-t
b
|的最小值为
3
2
．
（Ⅰ）若
c
=λ
a
+(1-λ)
b
，其中λ∈R，求|
c
|的最小值；
（Ⅱ）若
c
满足（
c
-
a
）（
c
-
b
）=
3
2
，求|
c
|的最大值．
已知二次函数f（x）的图象过点（0，4），对任意x满足f（3-x）=f（x），且有最小值是
7
4
．
（1）求f（x）的解析式；
（2）求函数h（x）=f（x）-（2t-3）x在区间[0，1]上的最小值，其中t∈R；
（3）在区间[-1，3]上，y=f（x）的图象恒在函数y=2x+m的图象上方，试确定实数m的范围．
已知函数f（x）=
2x3(x＜0)
-tanx(0≤x＜
π
2
)
，则f（f（
π
4
））=（　　）
A、1B、-2C、2D、-1
已知双曲线的中心是原点，焦点到渐近线的距离为2
3
，一条准线方程为y=-1，则其渐近线方程为
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网