题目内容
若一直角三角形的三边长构成公差为2的等差数列，则该直角三角形的周长为 ．
考点：等差数列的性质
专题：等差数列与等比数列
分析：根据题意和等差数列的定义，设设一直角三角形的三边长分别为：a、a+2、a+4，再由勾股定理列出方程求出a，进而求出三角形的周长．
解答：
解：由题意设一直角三角形的三边长分别为：a、a+2、a+4，
所以（a+4）2=a2+（a+2）2，即a2-4a-12=0，
解得，a=6或a=-2（舍去），
所以直角三角形的三边长分别为：6、8、10，
所以该直角三角形的周长为24，
故答案为：24．
所以（a+4）2=a2+（a+2）2，即a2-4a-12=0，
解得，a=6或a=-2（舍去），
所以直角三角形的三边长分别为：6、8、10，
所以该直角三角形的周长为24，
故答案为：24．
点评：本题考查等差数列的定义，以及勾股定理的应用，属于基础题．
练习册系列答案
相关题目
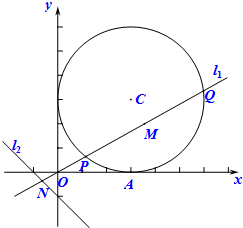已知圆C：（x-3）2+（y-3）2=9，直线l1：y=kx与圆C交于P、Q两个不同的点，M为P、Q的中点．