题目内容
某投资公司投资甲、乙两个项目所获得的利润分别P(亿元)Q(亿元),它们与各自的投资金x(亿元)之间的关系分别P(x)=
Q(x)=
x,今该公司将5亿元的资金投向这两个项目(允许全部投向某一个项目),其中对甲项目投资x(亿元),此次投资所获得的总利润为y(亿元).
(Ⅰ)写y关x的函数表达式并注明函数的定义域;
(Ⅱ)求总利润的最大值.
| 1 |
| 8 |
| 2x |
| 1 |
| 16 |
(Ⅰ)写y关x的函数表达式并注明函数的定义域;
(Ⅱ)求总利润的最大值.
考点:函数模型的选择与应用
专题:应用题,函数的性质及应用
分析:(Ⅰ)设甲项目投资x亿元,则乙项目投资(3-x)亿元,这两个项目所获得的总利润为y=M(亿元)+N(亿元),由经验公式代入整理即可;
(2)用换元法,再利用配方法,即可求总利润的最大值.
(2)用换元法,再利用配方法,即可求总利润的最大值.
解答:
解:(Ⅰ)设甲项目投资x亿元,则乙项目投资(5-x)亿元,这两个项目所获得的总利润为:y=
+
(5-x),x∈[0,5];
(Ⅱ)设t=
,t∈[0,
],则x=
t2,
∴y=
(2t+5-
t2)=-
(t-2)2+
;
∴当t=2,即x=2时,y有最大值为
.
| 1 |
| 8 |
| 2x |
| 1 |
| 16 |
(Ⅱ)设t=
| 2x |
| 10 |
| 1 |
| 2 |
∴y=
| 1 |
| 16 |
| 1 |
| 2 |
| 1 |
| 32 |
| 7 |
| 16 |
∴当t=2,即x=2时,y有最大值为
| 7 |
| 16 |
点评:本题用换元法得到一元二次函数的解析式,所以利用二次函数的性质求其最大值,是基础题.

练习册系列答案
相关题目
函数y=log2x的反函数和y=log2
的反函数的图象关于( )
| 1 |
| x |
| A、x轴对称 | B、y轴对称 |
| C、y=x对称 | D、原点对称 |
函数f(x)=log3(2x2-8x+m)的定义域为R,则m的取值范围是( )
| A、(8,+∞) |
| B、(-∞,8] |
| C、[8,+∞) |
| D、(-∞,8) |
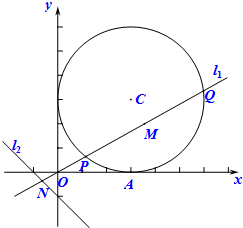 已知圆C:(x-3)2+(y-3)2=9,直线l1:y=kx与圆C交于P、Q两个不同的点,M为P、Q的中点.
已知圆C:(x-3)2+(y-3)2=9,直线l1:y=kx与圆C交于P、Q两个不同的点,M为P、Q的中点.