题目内容
若函数f(x)=a|x-b|+c满足①f(x+1)为偶函数;②在R上有大于零的最大值;③函数f(x)的图象过坐标原点;④a,b,c∈Z,试写出一组符合要求a,b,c的值 .
考点:带绝对值的函数
专题:计算题,函数的性质及应用
分析:由f(x+1)=a|x+1-b|+c为偶函数可得1-b=0,由在R上有大于零的最大值可得a<0,c>0,由函数f(x)的图象过坐标原点可得a+c=0,从而写出一组即可.
解答:
解:∵f(x+1)=a|x+1-b|+c为偶函数;
∴1-b=0,∴b=1;
∵在R上有大于零的最大值,
∴a<0,c>0,
又∵函数f(x)的图象过坐标原点,
∴a+c=0,
则由a,b,c∈Z可知,
符合上述要求a,b,c可以分别为:
-1,1,1.
故答案为:a=-1,b=1,c=1.
∴1-b=0,∴b=1;
∵在R上有大于零的最大值,
∴a<0,c>0,
又∵函数f(x)的图象过坐标原点,
∴a+c=0,
则由a,b,c∈Z可知,
符合上述要求a,b,c可以分别为:
-1,1,1.
故答案为:a=-1,b=1,c=1.
点评:本题考查了函数的性质应用,重点考查了绝对值函数的性质,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知函数①f(x)=5x2;②f(x)=5cosx;③f(x)=5ex;④f(x)=5lnx,其中对于f(x)定义域内的任意一个自变量x1,都存在唯一的自变量x2,使
=5成立的函数有( )个.
| f(x1)f(x2) |
| A、1个 | B、2个 | C、3个 | D、4个 |
已知平面向量
,
满足|
|=2,|
|=1,
与
夹角为60°,且2
-k
与
+
垂直,则实数k为( )
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| A、-5 | B、5 | C、4 | D、3 |
若椭圆的对称轴为坐标轴,长轴长与短轴长的和为18,焦距为6,则椭圆的方程为 ( )
A、
| ||||||||
B、
| ||||||||
C、
| ||||||||
D、
|
某几何体的三视图如图所示,且该几何体的体积是3,则正视图中的x的值是( )


| A、2 | ||
B、
| ||
C、
| ||
| D、3 |
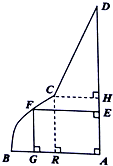 如图是一块镀锌铁皮的边角料ABCD,其中AB、CD、DA都是线段,曲线段BC是抛物线的一部分,且点B是该抛物线的顶点,BA所在直线是该抛物线的对称轴,经测量,AB=2米,AD=3米,AB⊥AD,点C到AD、AB的距离CH、CR的长均为1米,现要用这块边角料截一个矩形AEFG(其中点F在曲线段BC或线段CD上,点E在线段AD上,点G在线段AB上).设BG的长为x米,矩形AEFG的面积为S平方米.
如图是一块镀锌铁皮的边角料ABCD,其中AB、CD、DA都是线段,曲线段BC是抛物线的一部分,且点B是该抛物线的顶点,BA所在直线是该抛物线的对称轴,经测量,AB=2米,AD=3米,AB⊥AD,点C到AD、AB的距离CH、CR的长均为1米,现要用这块边角料截一个矩形AEFG(其中点F在曲线段BC或线段CD上,点E在线段AD上,点G在线段AB上).设BG的长为x米,矩形AEFG的面积为S平方米.