Question

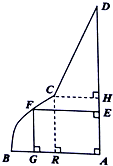如图是一块镀锌铁皮的边角料ABCD，其中AB、CD、DA都是线段，曲线段BC是抛物线的一部分，且点B是该抛物线的顶点，BA所在直线是该抛物线的对称轴，经测量，AB=2米，AD=3米，AB⊥AD，点C到AD、AB的距离CH、CR的长均为1米，现要用这块边角料截一个矩形AEFG（其中点F在曲线段BC或线段CD上，点E在线段AD上，点G在线段AB上）．设BG的长为x米，矩形AEFG的面积为S平方米．
（1）将S表示为x的函数；
（2）当x为多少米时，S取得最大值，最大值是多少？

Answer 1

考点：导数在最大值、最小值问题中的应用

专题：函数的性质及应用,导数的综合应用

分析：（1）由题意先根据已知条件建立平面直角坐标系，设出抛物线标准方程，然后将C点坐标给出来，代入方程求出p的值，然后分两段表示出S的值．
（2）按照分段函数求最值的方法，在两段上分别求出其最大值，然后大中取大，注意前一段利用导数研究单调性后求最值．后一段是二次函数的最值问题．

解答： 解：（1）以点B为坐标原点，BA所在直线为x轴，建立平面直角坐标系，
设曲线段BC所在抛物线方程为y²=2px（p＞0）．
将点C（1，1）代入，得2p=1．所以曲线段BC的方程为y=

x

（0≤x≤1）．
又由点C（1，1），D（2，3）得线段CD的方程为y=2x-1（1≤x≤2），
而GA=2-x，所以S=

x (2-x)，0≤x≤1 (2x-1)(2-x)，1＜x＜2

，
（2）①当0＜x≤1时，因为S=

x

(2-x)=2x

1

2

-x

3

2

，
所以S′=x-

1

2

-

3

2

x

1

2

=

2-3x

2 x

，令S′=0得x=

2

3

．
当x∈(0，

2

3

)时，S′＞0，所以此时S递增；
当x∈(

2

3

，1)时，S′＜0，所以此时S递减，所以当x=

2

3

时，Smax=

4 6

9

．
②当1＜x＜2时，因为S=(2x-1)(2-x)=-2(x-

5

4

)2+

9

8

．
所以当x=

5

4

时，Smax=

9

8

．
综上，因为

9

8

＞

4 6

9

，所以当x=

5

4

米时，Smax=

9

8

cm2．
答：当x取值为

5

4

米时，矩形AEFG的面积最大为

9

8

cm2．

点评：本题充分考查了分段函数的应用性问题，要注意抓住题目中的等量关系列出函数表达式，然后分两段研究其最值．