题目内容
某市物价局调查了治疗某种流感的常规药品在2012年每个月的批发价格和该药品在药店的销售价格,调查发现,该药品的批发价按月份以12元/盒为中心价随某一正弦曲线上下波动,且3月份的批发价格最高为14元/盒,7月份的批发价格最低为10元/盒.该药品在药店的销售价格按月份以14元/盒为中心价随另一正弦曲线上下波动,且5月份的销售价格最高为16元/盒,9月份的销售价格最低为12元/盒.
(1)求该药品每盒的批发价格f(x)和销售价格g(x)关于月份x的函数解析式;
(2)假设某药店每月初都购进这种药品p盒,且当月售完,求该药店在2012年哪些月份是盈利的?说明你的理由.
(1)求该药品每盒的批发价格f(x)和销售价格g(x)关于月份x的函数解析式;
(2)假设某药店每月初都购进这种药品p盒,且当月售完,求该药店在2012年哪些月份是盈利的?说明你的理由.
考点:函数模型的选择与应用
专题:计算题,应用题,函数的性质及应用,三角函数的图像与性质
分析:(1)由题意,设f(x)=A1sin(?1x+φ1)+12,g(x)=A2sin(?2x+φ2)+14,由题意确定参数即可;
(2)解不等式g(x)-f(x)=2sin(
x-
)+14-(2sin(
x-
)+12)>0即可.
(2)解不等式g(x)-f(x)=2sin(
| π |
| 4 |
| 3π |
| 4 |
| π |
| 4 |
| π |
| 4 |
解答:
解:(1)由题意,设f(x)=A1sin(?1x+φ1)+12,g(x)=A2sin(?2x+φ2)+14,
其中A1=
=2,?1=
=
,
故由f(3)=2sin(
×3+φ1)+12=14得,
φ1=-
;
故f(x)=2sin(
x-
)+12;
同理可得,
g(x)=2sin(
x-
)+14,(1≤x≤12,x∈N);
(2)g(x)-f(x)=2sin(
x-
)+14-(2sin(
x-
)+12)>0,
即sin
x<
;
又∵1≤x≤12,x∈N,
∴x=4,5,6,7,8,12;
即该药店在2012年的4,5,6,7,8,12月份是盈利的.
其中A1=
| 14-10 |
| 2 |
| 2π |
| 2×(7-3) |
| π |
| 4 |
故由f(3)=2sin(
| π |
| 4 |
φ1=-
| π |
| 4 |
故f(x)=2sin(
| π |
| 4 |
| π |
| 4 |
同理可得,
g(x)=2sin(
| π |
| 4 |
| 3π |
| 4 |
(2)g(x)-f(x)=2sin(
| π |
| 4 |
| 3π |
| 4 |
| π |
| 4 |
| π |
| 4 |
即sin
| π |
| 4 |
| ||
| 2 |
又∵1≤x≤12,x∈N,
∴x=4,5,6,7,8,12;
即该药店在2012年的4,5,6,7,8,12月份是盈利的.
点评:本题考查了三角函数在实际问题中的应用及三角恒等变换,属于中档题.

练习册系列答案
相关题目
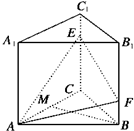 如图,在正三棱柱ABC-A1B1C1中,点E,F分别是棱CC1、BB1上的点,点M是线段AC上的动点,且满足EC=AB=2BF=2cm,当点M在什么位置时,MB∥平面AEF?并求截面AEF的面积.
如图,在正三棱柱ABC-A1B1C1中,点E,F分别是棱CC1、BB1上的点,点M是线段AC上的动点,且满足EC=AB=2BF=2cm,当点M在什么位置时,MB∥平面AEF?并求截面AEF的面积.