题目内容
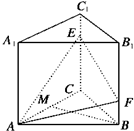 如图,在正三棱柱ABC-A1B1C1中,点E,F分别是棱CC1、BB1上的点,点M是线段AC上的动点,且满足EC=AB=2BF=2cm,当点M在什么位置时,MB∥平面AEF?并求截面AEF的面积.
如图,在正三棱柱ABC-A1B1C1中,点E,F分别是棱CC1、BB1上的点,点M是线段AC上的动点,且满足EC=AB=2BF=2cm,当点M在什么位置时,MB∥平面AEF?并求截面AEF的面积.考点:直线与平面平行的判定
专题:计算题,解三角形,空间位置关系与距离
分析:利用线面平行的判定定理即可得出当点M是线段AC中点时,BM∥平面AEF;然后分别求出AF,AE,EF的值,由余弦定理求出cos∠EFA,根据同角三角函数关系式求出sin∠EFA,根据三角形面积公式即可求值.
解答:
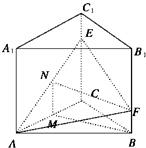 解:当点M是线段AC中点时,BM∥平面AEF.
解:当点M是线段AC中点时,BM∥平面AEF.
下面给出证明:
取AE中点N,连接NF、MN.
则MN
EC
FB,
∴MNFB是平行四边形,
则BM∥NF,
又∵NF?AEF,BM?平面AEF,
∴BM∥平面AEF.
∵正三棱柱ABC-A1B1C1中,EC=AB=2BF=2cm,
∴AF=
=
,AE=
=2
,EF=
=
,
∴由余弦定理知,△AEF中,cos∠EFA=
=
=
,可解得sin∠EFA=
=
,
∴S△AEF=
EF×AF×sin∠EFA=
×
×
×
=
.
 解:当点M是线段AC中点时,BM∥平面AEF.
解:当点M是线段AC中点时,BM∥平面AEF.下面给出证明:
取AE中点N,连接NF、MN.
则MN
| ∥ |
. |
| 1 |
| 2 |
| ∥ |
. |
∴MNFB是平行四边形,
则BM∥NF,
又∵NF?AEF,BM?平面AEF,
∴BM∥平面AEF.
∵正三棱柱ABC-A1B1C1中,EC=AB=2BF=2cm,
∴AF=
| AB2+BF2 |
| 5 |
| AC2+CE2 |
| 2 |
| (EC-BF)2+BC2 |
| 5 |
∴由余弦定理知,△AEF中,cos∠EFA=
| EF2+AF2-AE2 |
| 2×EF×AF |
| 5+5-8 | ||||
2×
|
| 1 |
| 5 |
| 1-cos2∠EFA |
2
| ||
| 5 |
∴S△AEF=
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 5 |
2
| ||
| 5 |
| 6 |
点评:本题考察了线面平行的判定定理、平行四边形的定义及三角形的中位线定理,熟练应用相关定理是解题的关键,属于基本知识的考查.

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
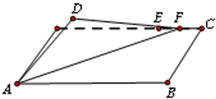 如图,在长方形ABCD中,AB=4,BC=1,E为DC的四等分点(靠近C处),F为线段EC上一动点(包括端点),现将△AFD沿AF折起,使D点在平面内的射影恰好落在边AB上,则当F运动时,二面角D-AF-B的平面角余弦值的变化范围为
如图,在长方形ABCD中,AB=4,BC=1,E为DC的四等分点(靠近C处),F为线段EC上一动点(包括端点),现将△AFD沿AF折起,使D点在平面内的射影恰好落在边AB上,则当F运动时,二面角D-AF-B的平面角余弦值的变化范围为