题目内容
已知直线与椭圆
+
=1交于A,B两点,设线段AB的中点为P,若直线的斜率为k1,直线OP的斜率为k2,则k1k2等于 .
| x2 |
| 9 |
| y2 |
| 4 |
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线的定义、性质与方程
分析:利用“平方差法”、线段中点坐标公式、斜率计算公式即可得出.
解答:
解:设A(x1,y1),B(x2,y2),P(x0,y0).则
=x0,
=y0,
=k1,k2=
.
∴
+
=1,
+
=1.两式作差并化简得
∴(x1+x2)(x1-x2)+
(y1+y2)(y1-y2)=0.
∴2x0+
×2y0•k1=0,
∴
+k1k2=0,
∴k1k2=--
.
故答案为:-
| x1+x2 |
| 2 |
| y1+y2 |
| 2 |
| y2-y1 |
| x2-x1 |
| y0 |
| x0 |
∴
| x12 |
| 9 |
| y12 |
| 4 |
| x22 |
| 9 |
| y22 |
| 4 |
∴(x1+x2)(x1-x2)+
| 9 |
| 4 |
∴2x0+
| 9 |
| 4 |
∴
| 9 |
| 4 |
∴k1k2=--
| 4 |
| 9 |
故答案为:-
| 4 |
| 9 |
点评:本题考查了“平方差法”、设而不求,以及线段中点坐标公式、斜率计算公式的应用,属于中档题.

练习册系列答案
相关题目
在区间[-2,2]上随机取一个数m,则直线y=x+m与圆x2+y2=2x相交的概率为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
向边长分别为5,6,
的三角形区域内随机投一点M,则该点M与三角形三个顶点距离都大于1的概率为( )
| 13 |
A、1-
| ||
B、1-
| ||
C、1-
| ||
D、1-
|
一简单组合体的三视图如图所示,则该组合体的体积为( )


| A、16-π | B、12-4π |
| C、12-2π | D、12-π |
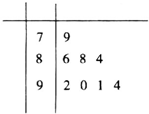 某校对高一年级8个班参加合唱比赛的得分进行了统计,得到样本的茎叶图(如图所示),则该样本的中位数和平均数分别是
某校对高一年级8个班参加合唱比赛的得分进行了统计,得到样本的茎叶图(如图所示),则该样本的中位数和平均数分别是