题目内容
已知函数f(x)=log
(8-2x)的定义域为(-∞,2].求函数f(x)的值域.
| 1 |
| 2 |
考点:复合函数的单调性,函数的值域
专题:函数的性质及应用
分析:利用函数的定义域,求出真数的范围,通过复合函数的单调性求出函数的最值.
解答:
解:函数f(x)=log
(8-2x)的定义域为(-∞,2].
所以2x≤4,∴8-2x≥4,
∴f(x)=log
(8-2x)≤log
4=-2.
函数的值域为(-∞,2].
| 1 |
| 2 |
所以2x≤4,∴8-2x≥4,
∴f(x)=log
| 1 |
| 2 |
| 1 |
| 2 |
函数的值域为(-∞,2].
点评:本题考查复合函数的单调性,函数的值域的求法,考查计算能力.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案
相关题目
如果等比数列{an}中,a2a4=16,那么a1•a3•a5=( )
| A、±4 | B、4 | C、±64 | D、64 |
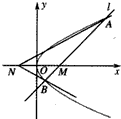 已知过点M(a,0)(a>0)的动直线l交抛物线y2=4x于A、B两点,点N与点M关于y轴对称,
已知过点M(a,0)(a>0)的动直线l交抛物线y2=4x于A、B两点,点N与点M关于y轴对称,