题目内容
已知函数f(x)=Asin(2x+
)+B(A>0)的最大值为2,最小值为0.
(1)求f(
)的值;
(2)将函数y=f(x)图象向右平移
个单位后,再将图象上所有点的纵坐标扩大到原来的
倍,横坐标不变,得到函数y=g(x)的图象,求方程g(x)=1的解.
| π |
| 4 |
(1)求f(
| 5π |
| 24 |
(2)将函数y=f(x)图象向右平移
| π |
| 4 |
| 2 |
考点:函数y=Asin(ωx+φ)的图象变换,正弦函数的图象
专题:三角函数的图像与性质
分析:(1)由题意可得B=
=1,A=
=1,求得 函数f(x)的解析式,从而求得f(
)的值.
(2)根据y=Asin(ωx+φ)的图象变换规律,得到函数y=g(x)=
sin(2x-
),由方程可得sin(2x-
)=
,由此解得x的值.
| 2+0 |
| 2 |
| 2-0 |
| 2 |
| 5π |
| 24 |
(2)根据y=Asin(ωx+φ)的图象变换规律,得到函数y=g(x)=
| 2 |
| π |
| 4 |
| π |
| 4 |
| ||
| 2 |
解答:
解:(1)由题意可得B=
=1,A=
=1,∴函数f(x)=sin(2x+
)+1,
∴f(
)=sin(
+
)+1=sin
+1=
+1.
(2)将函数y=f(x)图象向右平移
个单位后,可得函数y=sin[2(x-
)+
]+1=sin(2x-
)的图象,
再将图象上所有点的纵坐标扩大到原来的
倍,横坐标不变,
得到函数y=g(x)=
sin(2x-
)的图象.
由方程g(x)=1,可得sin(2x-
)=
,∴2x-
=2kπ+
,或2x-
=2kπ+
,k∈z.
解得x=kπ+
,或x=kπ+
k∈z.
即方程g(x)=1的解为{x|x=kπ+
,或x=kπ+
,k∈z}.
| 2+0 |
| 2 |
| 2-0 |
| 2 |
| π |
| 4 |
∴f(
| 5π |
| 24 |
| 5π |
| 12 |
| π |
| 4 |
| 2π |
| 3 |
| ||
| 2 |
(2)将函数y=f(x)图象向右平移
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
再将图象上所有点的纵坐标扩大到原来的
| 2 |
得到函数y=g(x)=
| 2 |
| π |
| 4 |
由方程g(x)=1,可得sin(2x-
| π |
| 4 |
| ||
| 2 |
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
| 3π |
| 4 |
解得x=kπ+
| π |
| 4 |
| π |
| 2 |
即方程g(x)=1的解为{x|x=kπ+
| π |
| 4 |
| π |
| 2 |
点评:本题主要考查利用y=Asin(ωx+φ)的图象特征,由函数y=Asin(ωx+φ)的部分图象求解析式,y=Asin(ωx+φ)的图象变换规律,三角方程的解法,属于中档题.

练习册系列答案
相关题目
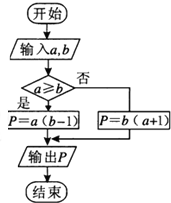 定义一种运算符号“?”,两个实数a,b的“a?b”运算原理如图所示,若输入a=2cos
定义一种运算符号“?”,两个实数a,b的“a?b”运算原理如图所示,若输入a=2cos