题目内容
小明给一个动点P编写了一个运动程序:给参量m赋予一个值后,点P将按如下设置的横、纵坐标程序运动.
参量m→赋值→(执行程序)→P(m-1,m2-2m)
(1)求点P运动轨迹所对应的解析式;
(2)在平面直角坐标系中画出点P的运动轨迹;
(3)当给参量m赋什么值时,点P在x轴的上方运动?
参量m→赋值→(执行程序)→P(m-1,m2-2m)
(1)求点P运动轨迹所对应的解析式;
(2)在平面直角坐标系中画出点P的运动轨迹;
(3)当给参量m赋什么值时,点P在x轴的上方运动?
考点:轨迹方程
专题:消元法,高考数学专题,圆锥曲线的定义、性质与方程,坐标系和参数方程
分析:(1)分别设x=m-1,y=m2-2m,消掉m问题就得以解决.
(2)通过函数的解析式可以看出是一条抛物线,画图就可以.
(3)p点在x轴的上方,也就是y>0,解不等式得到答案.
(2)通过函数的解析式可以看出是一条抛物线,画图就可以.
(3)p点在x轴的上方,也就是y>0,解不等式得到答案.
解答:
解:(1)∵x=m-1,y=m2-2m,则m=x+1,代入y=m2-2m得,y=(x+1)2-2(x+1)=x2-1,
(2)点的运动轨迹是一条抛物线,如图所示:

(3)∵p点在x轴的上方,
∴y>0,
即m2-2m>0,
即m(m-2)>0,
解得m>2,或m<0.
(2)点的运动轨迹是一条抛物线,如图所示:

(3)∵p点在x轴的上方,
∴y>0,
即m2-2m>0,
即m(m-2)>0,
解得m>2,或m<0.
点评:本题考查函数的解析式的常规求法,是中档题.解题时要认真审题,仔细解答.

练习册系列答案
相关题目
设某几何体的三视图如图所示,则该几何体的体积为( )
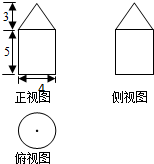

| A、24π | B、32π |
| C、52π | D、96π |
 如图,焦点在x轴上的椭圆T1与焦点在y轴上的椭圆T2相切于点M(0,1),且椭圆T1与T2的离心率均为
如图,焦点在x轴上的椭圆T1与焦点在y轴上的椭圆T2相切于点M(0,1),且椭圆T1与T2的离心率均为