题目内容
在圆的一条直径上,任取一点作与该直径垂直的弦,则其弦长超过该圆的内接等边三角形的边长概率为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:几何概型
专题:概率与统计
分析:由题意可得:如图,要使弦长大于CD的长,就必须使圆心O到弦的距离小于|OF|,即可得出结论、
解答:
解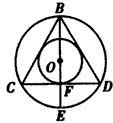 :如图所示,△BCD是圆内接等边三角形,
:如图所示,△BCD是圆内接等边三角形,
过直径BE上任一点作垂直于直径的弦,设大圆的半径为2,则等边三角形BCD的内切圆的半径为1,
显然当弦为CD时就是△BCD的边长,
要使弦长大于CD的长,就必须使圆心O到弦的距离小于|OF|,
记事件A={弦长超过圆内接等边三角形的边长}={弦中点在内切圆内},
由几何概型概率公式得P(A)=
=
,
即弦长超过圆内接等边三角形边长的概率是
.
故选C.
 :如图所示,△BCD是圆内接等边三角形,
:如图所示,△BCD是圆内接等边三角形,过直径BE上任一点作垂直于直径的弦,设大圆的半径为2,则等边三角形BCD的内切圆的半径为1,
显然当弦为CD时就是△BCD的边长,
要使弦长大于CD的长,就必须使圆心O到弦的距离小于|OF|,
记事件A={弦长超过圆内接等边三角形的边长}={弦中点在内切圆内},
由几何概型概率公式得P(A)=
| ||
| 2 |
| 1 |
| 2 |
即弦长超过圆内接等边三角形边长的概率是
| 1 |
| 2 |
故选C.
点评:本题考查了几何概型的运用;关键是找到事件A对应的集合,利用几何概型公式解答.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
执行如图所示的程序框图,输出s的值等于( )


| A、98 | B、100 |
| C、2450 | D、2550 |
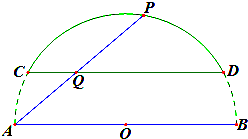 某房地产开发商在其开发的一个小区前面建了一个弓形景观湖,如图,该弓形所在的圆是以AB为直径的圆,已知AB=300m,CD与AB平行且它们之间的距离为50
某房地产开发商在其开发的一个小区前面建了一个弓形景观湖,如图,该弓形所在的圆是以AB为直径的圆,已知AB=300m,CD与AB平行且它们之间的距离为50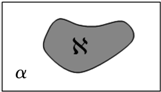 假定平面内的一条直线将该平面内的一个区域分成面积相等的两个区域,则称这条直线平分这个区域.如图,?是平面α内的任意一个封闭区域.现给出如下结论:
假定平面内的一条直线将该平面内的一个区域分成面积相等的两个区域,则称这条直线平分这个区域.如图,?是平面α内的任意一个封闭区域.现给出如下结论: