题目内容
已知数列{an}为等差数列，a1=1，公差d≠0，a1、a2、a5成等比数列，则a2014的值为 ．
考点：等差数列与等比数列的综合
专题：等差数列与等比数列
分析：利用等差数列与等比数列的通项公式即可得出．
解答：
解：∵a1、a2、a5成等比数列，∴a22=a1•a5，
∴（1+d）2=1×（1+4d），d≠0．
解得d=2．
∴a2014=a1+2013d=1+2013×2=4027，
故答案为：4027；
∴（1+d）2=1×（1+4d），d≠0．
解得d=2．
∴a2014=a1+2013d=1+2013×2=4027，
故答案为：4027；
点评：本题考查了等差数列与等比数列的通项公式，属于基础题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
过点P（-4，4）作直线l与圆O：x2+y2=4相交于A、B两点．在圆的一条直径上，任取一点作与该直径垂直的弦，则其弦长超过该圆的内接等边三角形的边长概率为（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
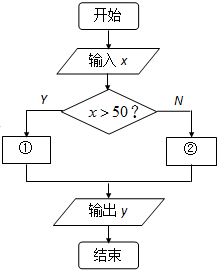某铁路客运部门规定甲、乙两地之间旅客托运行李的费用为：不超过50kg按0.53元/kg收费，超过50kg的部分按0.85元/kg收费．相应收费系统的流程图如右图所示，则①处应填（ ）| A、y=0.85x |
| B、y=0.53x |
| C、y=50×0.53+（x-50）×0.85 |
| D、y=50×0.53+0.85x |