题目内容
17.已知△ABC的顶点B、C在椭圆$\frac{x^2}{12}+\frac{y^2}{3}=1$上,顶点A是椭圆的一个焦点,且椭圆的另外一个焦点在BC边上,则△ABC的周长是( )| A. | $8\sqrt{3}$ | B. | 6 | C. | $4\sqrt{3}$ | D. | 12 |
分析 由题意知a=2$\sqrt{3}$,由椭圆的定义知AB+AC+BC=AB+BF+AC+FC=4a.
解答  解:∵椭圆的方程为$\frac{x^2}{12}+\frac{y^2}{3}=1$,
解:∵椭圆的方程为$\frac{x^2}{12}+\frac{y^2}{3}=1$,
∴a=2$\sqrt{3}$,
设椭圆的另外一个焦点为F,
∵顶点A是椭圆的一个焦点,且椭圆的另外一个焦点在BC边上,
∴AB+AC+BC
=AB+AC+BF+FC
=AB+BF+AC+FC
=2a+2a=4a=8$\sqrt{3}$,
故选:A.
点评 本题考查了椭圆的定义及数形结合的思想应用.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
7.从字母a、b、c、d、e中任取两个不同的字母,则取到字母a的概率为( )
| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
5.在正方形ABCD之内随机选取一点M到点D的距离小于正方形的边长的概率是( )
| A. | $\frac{π}{2}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{6}$ |
12.已知一组数据的频率分布直方图如图所示.求众数、中位数、平均数( )
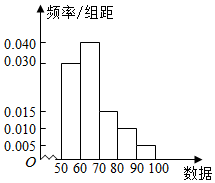

| A. | 63、64、66 | B. | 65、65、67 | C. | 65、64、66 | D. | 64、65、64 |
2.三棱柱ABC-A1B1C1中,侧棱AA1丄底面A1B1C1,底面三角形是正三角形,E是BC中点,则下列叙述正确的是( )
| A. | CC1与B1E是异面直线 | B. | AC丄平面ABB1A1 | ||
| C. | AE 丄 B1C1 | D. | A1C1∥平面AB1E |