题目内容
19.下列函数是正态分布密度函数的是( )| A. | f(x)=$\frac{1}{{\sqrt{2π}σ}}{e^{\frac{{{{(x-r)}^2}}}{2σ}}}$ | B. | f(x)=$\frac{{\sqrt{2π}}}{2π}{e^{-\frac{x^2}{2}}}$ | ||
| C. | f(x)=$\frac{1}{{2\sqrt{2}π}}{e^{\frac{{{{(x-1)}^2}}}{4}}}$ | D. | f(x)=$\frac{1}{{\sqrt{2π}}}{e^{\frac{x^2}{2}}}$ |
分析 直接在正态密度函数f(x)=$\frac{1}{\sqrt{2π}δ}{e}^{-\frac{(x-μ)^{2}}{2{δ}^{2}}}$中去μ=0,δ=1得答案.
解答 解:由正态密度函数的特征f(x)=$\frac{1}{\sqrt{2π}δ}{e}^{-\frac{(x-μ)^{2}}{2{δ}^{2}}}$可知,
当δ=1,μ=0时,正态密度函数f(x)=$\frac{1}{\sqrt{2π}δ}{e}^{-\frac{(x-μ)^{2}}{2{δ}^{2}}}$=$\frac{{\sqrt{2π}}}{2π}{e^{-\frac{x^2}{2}}}$=$\frac{1}{\sqrt{2π}}{e}^{-\frac{{x}^{2}}{2}}$为标准正态密度函数,
故选:B.
点评 本题考查正态分布曲线的特点及曲线所表示的意义,关键是熟记正态密度函数的特征,是基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
7.从字母a、b、c、d、e中任取两个不同的字母,则取到字母a的概率为( )
| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
14.下列函数是偶函数的是( )
| A. | y=x2,x∈[0,1] | B. | y=x3 | C. | y=2x2-3 | D. | y=x |
11.函数$y=2sin(x+\frac{π}{3})$的图象的一个对称中心是( )
| A. | (0,0) | B. | $(-\frac{π}{3},0)$ | C. | $(\frac{π}{3},0)$ | D. | $(\frac{π}{6},0)$ |
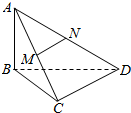 如图所示,已知AB⊥平面BCD,M,N分别是AC,AD的中点,BC⊥CD.
如图所示,已知AB⊥平面BCD,M,N分别是AC,AD的中点,BC⊥CD.