题目内容
定义:若一个数列每相邻两项的和都等于同一个常数,则称这个数列为等和数列,这个常数叫做公和.同样道理,若一个数列每相邻两项的积都等于同一个常数,则称这个数列为等积数列,这个常数叫做公积,已知数列{an}是首项为1,公和为4的等和数列,前n项和为Sn,数列{bn}是首项为1,公积为4的等积数列,前n项和为
Tn,则
= .
Tn,则
| S2012 |
| T2012 |
考点:等差数列与等比数列的综合
专题:等差数列与等比数列
分析:由题意可得,an+an+1=4,bnbn+1=4,由递推公式可求解数列的通项公式,进而求得数列的和.
解答:
解:由题意可得,
an+an+1=4,a1=1,
∴a2=3,a3=1,a4=3,…
∴an=
,
∴s2012=
(1+3)=4024
又bnbn+1=4,
∵b1=1
∴b2=4,b3=1,b4=4,…,
∴bn=
,
∴T2012=
(1+4)=5030,
∴
=
=
.
故答案为:
.
an+an+1=4,a1=1,
∴a2=3,a3=1,a4=3,…
∴an=
|
∴s2012=
| 2012 |
| 2 |
又bnbn+1=4,
∵b1=1
∴b2=4,b3=1,b4=4,…,
∴bn=
|
∴T2012=
| 2012 |
| 2 |
∴
| S2012 |
| T2012 |
| 4024 |
| 5030 |
| 4 |
| 5 |
故答案为:
| 4 |
| 5 |
点评:此题的思想方法要抓住给出的信息,观察数列的规律,总结出项数与项之间的关系,求出通项公式时需要分类讨论,一定清楚奇数项数与偶数项数,否则容易出错.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知函数f(x)=2x+sinx,若f(2x-y+3)≤0,则x2+y2的最小值为( )
A、
| ||||
B、3
| ||||
C、
| ||||
D、
|
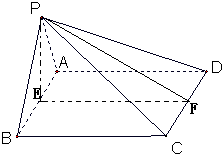 如图,四棱锥P-ABCD的底面是矩形,侧面PAB是等边三角形,AB、CD中点分别为E、F,侧面PAB⊥底面ABCD.
如图,四棱锥P-ABCD的底面是矩形,侧面PAB是等边三角形,AB、CD中点分别为E、F,侧面PAB⊥底面ABCD.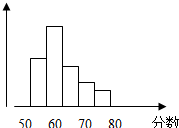 某中学举行电脑知识竞赛,满分为100分,80分以上为优秀(含80分)现将高一两个班参赛学生的成绩进行整理后分成5组,绘制成频率分布直方图如图所示.已知图中从左到右的第一、三、四、五小组的频率分别为 0.30、0.15、10、0.05,而第二小组的频数是40,则参赛的人数是
某中学举行电脑知识竞赛,满分为100分,80分以上为优秀(含80分)现将高一两个班参赛学生的成绩进行整理后分成5组,绘制成频率分布直方图如图所示.已知图中从左到右的第一、三、四、五小组的频率分别为 0.30、0.15、10、0.05,而第二小组的频数是40,则参赛的人数是