题目内容
已知F1、F2分别为椭圆
+
=1﹙a＞b＞0﹚的左、右焦点，M、N分别为其左右顶点，过F2的直线L与椭圆相交于A、B两点，当直线L与x轴垂直时，四边形AMBN的面积等于 ．
| x2 |
| a2 |
| y2 |
| b2 |
考点：直线与圆锥曲线的关系
专题：圆锥曲线的定义、性质与方程
分析：当直线L与x轴垂直时，把x=c代入椭圆方程可得：
+
=1，解得A，B的坐标．可得|AB|．利用四边形AMBN的面积S=
|MN||AB|即可得出．
| c2 |
| a2 |
| y2 |
| b2 |
| 1 |
| 2 |
解答：
解：当直线L与x轴垂直时，把x=c代入椭圆方程可得：
+
=1，解得y=±
．
∴|AB|=
．
∴四边形AMBN的面积S=
|MN||AB|=
×2a×
=2b2．
故答案为：2b2．
| c2 |
| a2 |
| y2 |
| b2 |
| b2 |
| a |
∴|AB|=
| 2b2 |
| a |
∴四边形AMBN的面积S=
| 1 |
| 2 |
| 1 |
| 2 |
| 2b2 |
| a |
故答案为：2b2．
点评：本题考查了直线与椭圆相交弦长问题、四边形的面积计算公式，考查了计算能力，属于基础题．
练习册系列答案
激活思维优加课堂系列答案
活力试卷系列答案
相关题目
已知集合B={-1，1，4}满足条件∅?M⊆B的集合M的个数为（ ）
| A、3 | B、6 | C、7 | D、8 |
已知函数f（x）=ax2-2x-a+
，若存在x0∈[1，4]，使f（x0）=0有解，则实数a的取值范围是（ ）
| 5 |
| 2 |
| A、（-∞，2） | ||
B、（0，
| ||
C、[
| ||
D、（-∞，
|
已知集合M={-1，0，2}，N={x|
≤0}，则M∩N=（ ）
| x-2 |
| x+1 |
| A、{-1，0，2} |
| B、{0，1，2} |
| C、{0，2} |
| D、∅ |
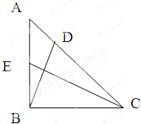等腰直角三角形ABC中，AB=BC=2，