题目内容
已知椭圆C两焦点坐标分别为F1(-
,0),F2(
,0),一个顶点为A(0,-1).
(1)求椭圆C的标准方程;
(2)是否存在斜率为k(k≠0)的直线l,使直线l与椭圆C交于不同的两点M,N,满足|AM|=|AN|.若存在,求出k的取值范围;若不存在,说明理由.
| 2 |
| 2 |
(1)求椭圆C的标准方程;
(2)是否存在斜率为k(k≠0)的直线l,使直线l与椭圆C交于不同的两点M,N,满足|AM|=|AN|.若存在,求出k的取值范围;若不存在,说明理由.
考点:直线与圆锥曲线的综合问题
专题:综合题,圆锥曲线的定义、性质与方程
分析:(Ⅰ)根据椭圆C两焦点坐标和一个顶点A(0,-1).因此可设椭圆方程
+
=1(a>b>0).得到c,b,再利用a2=b2+c2即可.
(II)假设存在这样的直线l.设直线l的方程为y=kx+m,与椭圆的方程联立可得(1+3k2)x2+6kmx+3m2-3=0,得到△>0.设M(x1,y1),N(x2,y2),线段MN中点为P(x0,y0),得到根与系数的关系,再利用中点坐标公式可得P的坐标.由于|AM|=|AN|,可得AP⊥MN,于是kAP•k=-1即可得出.
| x2 |
| a2 |
| y2 |
| b2 |
(II)假设存在这样的直线l.设直线l的方程为y=kx+m,与椭圆的方程联立可得(1+3k2)x2+6kmx+3m2-3=0,得到△>0.设M(x1,y1),N(x2,y2),线段MN中点为P(x0,y0),得到根与系数的关系,再利用中点坐标公式可得P的坐标.由于|AM|=|AN|,可得AP⊥MN,于是kAP•k=-1即可得出.
解答:
解:(Ⅰ)∵椭圆C两焦点坐标分别为F1(-
,0),F2(
,0),一个顶点为A(0,-1).
∴可设椭圆方程为
+
=1(a>b>0).
∴c=
,b=1,
∴a2=b2+c2=3.
∴椭圆C的方程为
+y2=1.
(Ⅱ)存在这样的直线l.
设直线l的方程为y=kx+m,代入椭圆方程化为(1+3k2)x2+6kmx+3m2-3=0
∵△=36k2m2-4(1+3k2)(3m2-3)得3k2-m2+1>0…①
设M(x1,y1),N(x2,y2),线段MN中点为P(x0,y0),
则x1+x2=-
,x1x2=
.
于是x0=-
,y0=kx0+m=
.
∵|AM|=|AN|,∴AP⊥MN.
若m=0,则直线l过原点,P(0,0),不合题意.
若m≠0,由k≠0得,kAP•k=-1得到
•k=-1,整理得2m=3k2+1…②
由①②知,k2<1,∴-1<k<1.
又k≠0,∴k∈(-1,0)∪(0,1).
| 2 |
| 2 |
∴可设椭圆方程为
| x2 |
| a2 |
| y2 |
| b2 |
∴c=
| 2 |
∴a2=b2+c2=3.
∴椭圆C的方程为
| x2 |
| 3 |
(Ⅱ)存在这样的直线l.
设直线l的方程为y=kx+m,代入椭圆方程化为(1+3k2)x2+6kmx+3m2-3=0
∵△=36k2m2-4(1+3k2)(3m2-3)得3k2-m2+1>0…①
设M(x1,y1),N(x2,y2),线段MN中点为P(x0,y0),
则x1+x2=-
| 6km |
| 1+3k2 |
| 3m2-3 |
| 1+3k2 |
于是x0=-
| 3km |
| 1+3k2 |
| m |
| 1+3k2 |
∵|AM|=|AN|,∴AP⊥MN.
若m=0,则直线l过原点,P(0,0),不合题意.
若m≠0,由k≠0得,kAP•k=-1得到
| y0+1 |
| x0 |
由①②知,k2<1,∴-1<k<1.
又k≠0,∴k∈(-1,0)∪(0,1).
点评:本题考查了椭圆的标准方程及其性质、直线与椭圆相交问题转化为方程联立得到根与系数的关系、中点坐标公式、相互垂直的直线与斜率之间的关系等基础知识与基本技能方法,考查了推理能力和计算能力,属于难题.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案
相关题目
 某学校共有30至50岁之间的(包括30与不包括50)数学教师15人,其年龄分布茎叶图如图所示,从中选取3人参加支教.
某学校共有30至50岁之间的(包括30与不包括50)数学教师15人,其年龄分布茎叶图如图所示,从中选取3人参加支教.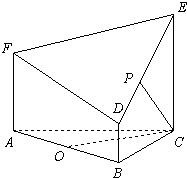 如图所示的几何体是由以等边三角形ABC为底面的棱柱被平面DEF所截而得,AB=2,BD=1,AF=a.
如图所示的几何体是由以等边三角形ABC为底面的棱柱被平面DEF所截而得,AB=2,BD=1,AF=a.