题目内容
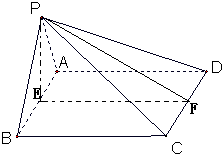 如图,四棱锥P-ABCD的底面是矩形,侧面PAB是等边三角形,AB、CD中点分别为E、F,侧面PAB⊥底面ABCD.
如图,四棱锥P-ABCD的底面是矩形,侧面PAB是等边三角形,AB、CD中点分别为E、F,侧面PAB⊥底面ABCD.(1)求证:面PAD⊥面PAB;
(2)求证CD⊥平面PEF.
考点:平面与平面垂直的性质
专题:空间位置关系与距离
分析:(1)首先,证明PE⊥AB,然后,得到PE⊥底面ABCD,最后,通过证明AD⊥平面PAB,得到面PAD⊥面PAB;
(2)首先,得到PE⊥底面ABCD,然后,证得AB⊥平面PEF,再结合AB∥CD,得到CD⊥平面PEF.
(2)首先,得到PE⊥底面ABCD,然后,证得AB⊥平面PEF,再结合AB∥CD,得到CD⊥平面PEF.
解答:
证明:(1)∵E为等边三角形边AB上的中点,
∴PE⊥AB,
又∵面PAB⊥底面ABCD.
∴PE⊥底面ABCD.
∴PE⊥AD,
又AD⊥AB,
∴AD⊥平面PAB,
∴面PAD⊥面PAB;
(2)由(1),得
PE⊥底面ABCD,
EF∥BC,
∴AB⊥EF,
∴AB⊥平面PEF,
又∵AB∥CD,
∴CD⊥平面PEF.
∴PE⊥AB,
又∵面PAB⊥底面ABCD.
∴PE⊥底面ABCD.
∴PE⊥AD,
又AD⊥AB,
∴AD⊥平面PAB,
∴面PAD⊥面PAB;
(2)由(1),得
PE⊥底面ABCD,
EF∥BC,
∴AB⊥EF,
∴AB⊥平面PEF,
又∵AB∥CD,
∴CD⊥平面PEF.
点评:本题重点考查了空间中点线面的位置关系,证明垂直关系时,一定注意等价转化思想的灵活运用.

练习册系列答案
 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案
相关题目
若a>b>0,且a+b=1,则下列式子中最大的是( )
| A、log2a+log2b+1 |
| B、log2a |
| C、log2(a2+b2) |
| D、-1 |
 某学校共有30至50岁之间的(包括30与不包括50)数学教师15人,其年龄分布茎叶图如图所示,从中选取3人参加支教.
某学校共有30至50岁之间的(包括30与不包括50)数学教师15人,其年龄分布茎叶图如图所示,从中选取3人参加支教.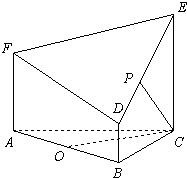 如图所示的几何体是由以等边三角形ABC为底面的棱柱被平面DEF所截而得,AB=2,BD=1,AF=a.
如图所示的几何体是由以等边三角形ABC为底面的棱柱被平面DEF所截而得,AB=2,BD=1,AF=a.