题目内容
3.对于函数f(x),若存在区间A=[m,n],使得{y|y=f(x),x∈A}=A,则称函数f(x)为“可等域函数”,区间A为函数f(x)的一个“可等域区间”,给出下列四个函数:①f(x)=sin($\frac{π}{2}$x)
②f(x)=|2x-1|
③f(x)=2x2-1
④f(x)=log2(2x-2).
其中存在唯一“可等域区间”的“可等域函数”的序号为②③.
分析 根据“可等域区间”的定义分别进行判断即可得到结论.
解答 解:①:函数f(x)=sin($\frac{π}{2}$x)的周期是4,正弦函数的性质我们易得,A=[0,1]为函数的一个“可等域区间”,同时当A=[-1,0]时也是函数的一个“可等域区间”,∴不满足唯一性.
②A=[0,1]为函数f(x)=|2x-1|的“可等域区间”,
当x∈[0,1]时,f(x)=2x-1,函数单调递增,f(0)=1-1=0,f(1)=2-1=1满足条件,
∴m,n取值唯一.故满足条件.
③当A=[-1,1]时,f(x)∈[-1,1],满足条件,且由二次函数的图象可知,满足条件的集合只有A=[-1,1]一个.
④∵f(x)=log2(2x-2)单调递增,且函数的定义域为(1,+∞),
若存在“可等域区间”,则满足$\left\{\begin{array}{l}{lo{g}_{2}(2m-2)=m}\\{lo{g}_{2}(2n-2)=n}\end{array}\right.$,即$\left\{\begin{array}{l}{2m-2={2}^{m}}\\{2n-2={2}^{n}}\end{array}\right.$,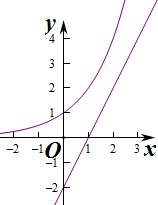
∴m,n是方程2x=2x-2的两个根,
作出函数设f(x)=2x和y=2x-2的图象,
当x>1时,两个函数没有交点,
∴f(x)=2x-2x+2=0不可能存在两个解,
故f(x)=log2(2x-2)不存在“可等域区间”.
故答案为:②③
点评 本题主要考查与函数有关的新定义问题,根据“可等域区间”的定义,建立条件关系是解决本题的关键,综合性较强,有一定的难度.

练习册系列答案
相关题目
11.已知集合A={x|2x>1},B={ x|x<1},则A∩B?( )
| A. | { x|0<x<1} | B. | { x|x>?0} | C. | { x|x>1} | D. | {x|x<1} |
18.一几何体的三视图如图所示,则该几何体的各个面中面积最大的面的面积为( )
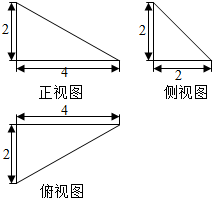

| A. | 4 | B. | 5 | C. | $\frac{9}{2}$ | D. | 6 |
8.设$\overrightarrow{e_1}$,$\overrightarrow{e_2}$,$\overrightarrow{e_3}$为单位向量,且$\overrightarrow{e_3}=\frac{1}{2}\overrightarrow{e_1}+k\overrightarrow{e_2}$,(k>0),若以向量$\overrightarrow{e_1}$,$\overrightarrow{e_2}$为两边的三角形的面积为$\frac{1}{2}$,则k的值为( )
| A. | $\frac{{\sqrt{2}}}{2}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $\frac{{\sqrt{5}}}{2}$ | D. | $\frac{{\sqrt{7}}}{2}$ |
15.若集合A={x|$\sqrt{x}$>2},B={x|1<x<5},则A∩B等于( )
| A. | (1,4) | B. | (4,5) | C. | (1,5) | D. | (5,+∞) |
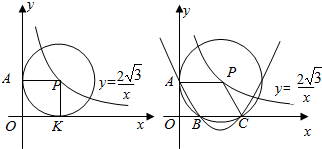 在直角坐标系xOy中,已知点P是反比例函数y=$\frac{2\sqrt{3}}{x}$(x>0)图象上一个动点,以P为圆心的圆始终与y轴相切,设切点为A.
在直角坐标系xOy中,已知点P是反比例函数y=$\frac{2\sqrt{3}}{x}$(x>0)图象上一个动点,以P为圆心的圆始终与y轴相切,设切点为A.