题目内容
已知函数f(x)=ax2+3x-2在点(2,f(2))处的切线斜率为7,则实数a的值为( )
| A、-1 | B、1 | C、±1 | D、-2 |
考点:利用导数研究曲线上某点切线方程
专题:导数的综合应用
分析:求出原函数的导函数,进一步求得f′(2),由f′(2)=7列式求解实数a的值.
解答:
解:f(x)=ax2+3x-2,
∴f′(x)=2ax+3.
又函数f(x)=ax2+3x-2在点(2,f(2))处的切线斜率为7,
∴f′(2)=4a+3=7,解得:a=1.
故选:B.
∴f′(x)=2ax+3.
又函数f(x)=ax2+3x-2在点(2,f(2))处的切线斜率为7,
∴f′(2)=4a+3=7,解得:a=1.
故选:B.
点评:本题考查利用导数研究曲线上某点处的切线方程,曲线上过某点的切线的斜率,就是该点处的导数值,是中档题.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案
相关题目
已知i为虚数单位,若
=y+2i,x,y∈R,则复数x+yi=( )
| x-i |
| i |
| A、2+i | B、-2-i |
| C、l-2i | D、1+2i |
已知数列{an}满足an+1=an-
,且a1=5,设{an}的n项和为Sn,则使得Sn取得最大值的序号n的值为( )
| 5 |
| 7 |
| A、7 | B、8 | C、7或8 | D、8或9 |
若a=log3π,b=(
)0.3,c=log20.8,则( )
| 1 |
| 2 |
| A、a>b>c |
| B、b>a>c |
| C、c>a>b |
| D、b>c>a |
设集合A={0,1,2,4,5,7},集合B={1,3,6,8,9},集合C={3,7,9},则集合(A∩B)∪C等于( )
| A、{3,7,9} |
| B、{3,6,7,9} |
| C、{1,3,7,9} |
| D、{0,1,2,6,9} |
不等式
≥0的解集是( )
| 2-x |
| x-1 |
| A、(-∞,1)∪[2,+∞) |
| B、(-∞,1]∪[2,+∞) |
| C、[1,2] |
| D、(1,2] |
幂函数f(x)的图象过点(4,2),那么f(8)的值为( )
A、2
| ||
B、2
| ||
| C、64 | ||
D、
|
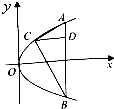 如图,直角三角形ABC的三个顶点在给定的抛物线y2=2px(p>0)上,斜边AB平行于y轴,则AB边上的高|CD|=
如图,直角三角形ABC的三个顶点在给定的抛物线y2=2px(p>0)上,斜边AB平行于y轴,则AB边上的高|CD|=