题目内容
给出命题：p：3＞5，q：4∈{2，4}，则在下列三个复合命题：“p∧q”，“p∨q”，“￢p”中，真命题的个数为（ ）
| A、0 | B、3 | C、2 | D、1 |
考点：复合命题的真假
专题：简易逻辑
分析：首先判断p，q的真假，然后根据复合命题的真值表一一加以判断，即可得到结论．
解答：
解：命题p：3＞5是假命题，命题q：4∈{2，4}是真命题，
∴由复合命题的真值表得：p∧q为假命题，p∨q为真命题，￢p是真命题．
故真命题的个数为2．
故选C．
∴由复合命题的真值表得：p∧q为假命题，p∨q为真命题，￢p是真命题．
故真命题的个数为2．
故选C．
点评：本题考查复合命题的真假判断，注意运用真值表加以判断，准确判断p，q的真假是解题的关键，本题是基础题．
练习册系列答案
阅读快车系列答案
相关题目
复数z=
-（i-1）（i+1）的模是（ ）
| 1 |
| i |
| A、1 | ||
B、
| ||
| C、2 | ||
D、
|
函数f（x）的图象如图，则f（x）的解析式可能是（ ）
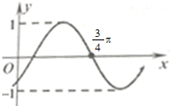
| A、f（x）=cos2x | ||||
B、f（x）=-sin（x+
| ||||
C、f（x）=cos（
| ||||
D、f（x）=sin（
|
如图是求10!的程序框图，则在判断框内应填的条件可以是（ ）| A、i＜10？ |
| B、i≤10？ |
| C、i≤11？ |
| D、i＞10？ |
下列函数中最小值为4的是（ ）
| A、y=4ex+e-x | ||||
B、y=x+
| ||||
C、y=
| ||||
| D、y=log3x+logx3（0＜x＜1） |
一个几何体的三视图如图所示，则该几何体的外接球的体积为（ ）
A、4
| ||
| B、12π | ||
C、2
| ||
D、4
|
已知函数f（x）=ax2+3x-2在点（2，f（2））处的切线斜率为7，则实数a的值为（ ）
| A、-1 | B、1 | C、±1 | D、-2 |
定义域为R的奇函数f（x），当x∈（-∞，0）时，f（x）+xf′（x）＜0恒成立，若a=3f（3），b=-f（-1），c=-2f（-2），则a，b，c的大小关系是（ ）
| A、a＞c＞b |
| B、c＞b＞a |
| C、c＞a＞b |
| D、a＞b＞c |