题目内容
在平面直角坐标系xoy中,已知圆C1:(x+3)2+(y-1)2=4和圆C2:(x-4)2+(y-5)2=4.若直线l过点A(4,0),且被圆C1截得的弦长为2
,求直线l的方程.
| 3 |
考点:直线与圆的位置关系,圆与圆的位置关系及其判定
专题:直线与圆
分析:根据直线和圆相交的弦长公式设出直线斜率,根据半弦长、半径、弦心距满足勾股定理,解方程求出k值,代入即得直线l的方程.
解答:
解:由于直线x=4与圆C1不相交;
∴直线l的斜率存在,设l方程为:y=k(x-4),即kx-y-4k=0,
圆C1:(x+3)2+(y-1)2=4的半径r=2,
设圆C1的圆心到直线l的距离为d,
∵l被⊙C1截得的弦长为2
,
∴圆心(-3,1)到直线的距离d=
=
=1,
即
=
=1,
即k(24k+7)=0即k=0或k=-
,
∴直线l的方程为:y=0或7x+24y-28=0,
∴直线l的斜率存在,设l方程为:y=k(x-4),即kx-y-4k=0,
圆C1:(x+3)2+(y-1)2=4的半径r=2,
设圆C1的圆心到直线l的距离为d,
∵l被⊙C1截得的弦长为2
| 3 |
∴圆心(-3,1)到直线的距离d=
4-(
|
| 4-3 |
即
| |-3k-1-4k| | ||
|
| |7k+1| | ||
|
即k(24k+7)=0即k=0或k=-
| 7 |
| 24 |
∴直线l的方程为:y=0或7x+24y-28=0,
点评:本题主要考查直线方程的求解,根据直线和圆相交的弦长公式求出直线斜率是解决本题的关键.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
下列函数中,与函数y=x有相同图象的一个函数是( )
A、y=
| ||
B、y=
| ||
| C、y=logaax | ||
D、y=(
|
已知命题P:关于x的函数f(x)=2x2+ax+2,在区间[1,+∞)上是增函数,命题q:关于x的方程x2-ax+a=0有实数根.若p∨q为真命题,p∧q为假命题,则实数a的取值范围是( )
| A、(-4,4)∪(4,+∞) |
| B、(-∞,-4) |
| C、(-∞,-4)∪(0,4) |
| D、[-4,+∞) |
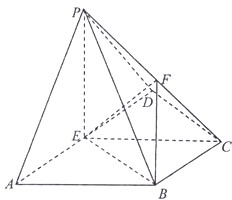 如图,在四棱锥P-ABCD中,侧面PAD⊥底面ABCD,ABCD是梯形,BC∥AD,E,F分别是AD,PC的中点,△ABE,△BEC,△ECD都是边长为1的等边三角形.
如图,在四棱锥P-ABCD中,侧面PAD⊥底面ABCD,ABCD是梯形,BC∥AD,E,F分别是AD,PC的中点,△ABE,△BEC,△ECD都是边长为1的等边三角形.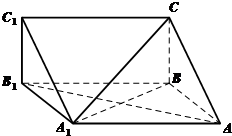 如图,在三棱柱ABC-A1B1C1中,AA1=AB,∠ABC=90°,侧面A1ABB1⊥底面ABC.
如图,在三棱柱ABC-A1B1C1中,AA1=AB,∠ABC=90°,侧面A1ABB1⊥底面ABC.