题目内容
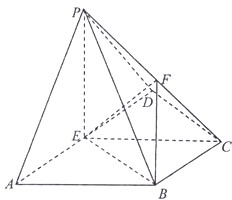 如图,在四棱锥P-ABCD中,侧面PAD⊥底面ABCD,ABCD是梯形,BC∥AD,E,F分别是AD,PC的中点,△ABE,△BEC,△ECD都是边长为1的等边三角形.
如图,在四棱锥P-ABCD中,侧面PAD⊥底面ABCD,ABCD是梯形,BC∥AD,E,F分别是AD,PC的中点,△ABE,△BEC,△ECD都是边长为1的等边三角形.(1)求证:AP∥平面EFB;
(2)若PA=PD,二面角F-EB-C的大小为
| π |
| 3 |
考点:二面角的平面角及求法,直线与平面平行的判定
专题:空间位置关系与距离,空间角
分析:(1)连AC交EB与O,连OF,由已知条件得ABCE为平行四边形,从而OF∥AP,由此能证明AP∥平面EFB.
(2)取BC中点G,以E为原点,EA为x轴,EG为y轴,建立空间直角坐标系,分别求出平面BEF的法向量和平面BEC的法向量,由已知条件求出
=(-
,
,
),再由平面PAD的法向量
=(0,1,0),利用向量法能求出点F到平面PAD的距离.
(2)取BC中点G,以E为原点,EA为x轴,EG为y轴,建立空间直角坐标系,分别求出平面BEF的法向量和平面BEC的法向量,由已知条件求出
| EF |
| 1 |
| 4 |
| ||
| 4 |
| 3 |
| 4 |
| p |
解答:
(1)证明:连AC交EB与O,连OF,
∵ABCD是梯形,BC∥AD,
E,F分别是AD,PC的中点,
△ABE,△BEC,△ECD都是边长为1的等边三角形,
∴AE
BC,∴ABCE为平行四边形,
∴O为AC中点,
∴在△APC中,OF∥AP,
又∵OF?平面EFB,AP?平面EFB,
∴AP∥平面EFB.
(2)解:取BC中点G,以E为原点,EA为x轴,
EG为y轴,建立空间直角坐标系,
E(0,0,0),B(
,
,0),
C(-
,
,0),设P(0,0,t),(t>0),则F(-
,
,
),
=(-
,
,
),
=(
,
,0),
设平面BEF的法向量
=(x,y,z),
则
,取x=
,得
=(
,-1,
),
又平面BEC的法向量
=(0,0,1),二面角F-EB-C的大小为
,
∴cos
=|cos<
,
>|=|
|=|
|=
,
由t>0,解得t=
.∴
=(-
,
,
),
又平面PAD的法向量
=(0,1,0),
∴点F到平面PAD的距离d=
=
=
.
故点F到平面PAD的距离为
.

∵ABCD是梯形,BC∥AD,
E,F分别是AD,PC的中点,
△ABE,△BEC,△ECD都是边长为1的等边三角形,
∴AE
| ∥ |
. |
∴O为AC中点,
∴在△APC中,OF∥AP,
又∵OF?平面EFB,AP?平面EFB,
∴AP∥平面EFB.
(2)解:取BC中点G,以E为原点,EA为x轴,
EG为y轴,建立空间直角坐标系,
E(0,0,0),B(
| 1 |
| 2 |
| ||
| 2 |
C(-
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 4 |
| ||
| 4 |
| t |
| 2 |
| EF |
| 1 |
| 4 |
| ||
| 4 |
| t |
| 2 |
| EB |
| 1 |
| 2 |
| ||
| 2 |
设平面BEF的法向量
| n |
则
|
| 3 |
| n |
| 3 |
| ||
| t |
又平面BEC的法向量
| m |
| π |
| 3 |
∴cos
| π |
| 3 |
| n |
| m |
| ||||
|
|
| ||||
|
| 1 |
| 2 |
由t>0,解得t=
| 3 |
| 2 |
| EF |
| 1 |
| 4 |
| ||
| 4 |
| 3 |
| 4 |
又平面PAD的法向量
| p |
∴点F到平面PAD的距离d=
|
| ||||
|
|
| ||||
| 1 |
| ||
| 4 |
故点F到平面PAD的距离为
| ||
| 4 |
点评:本题考查直线与平面平行的证明,考查点到平面的距离的求法,解题时要认真审题,注意空间思维能力的培养,注意向量法的合理运用.

练习册系列答案
相关题目
设全集U={1,2,3,4,5},A={x|x2-6x+5=0},则∁UA等于( )
| A、{3} |
| B、{2,3} |
| C、{2,4} |
| D、{2,3,4} |
已知等差数列{an}中,a1007=4,S2014=2014,则S2015=( )
| A、-2015 | B、2015 |
| C、-4030 | D、4030 |
已知命题p:?x>0,2x>1,则¬p为( )
| A、?x>0,2x≤1 |
| B、?x0>0,2 x0≤1 |
| C、?x0>0,2 x0>1 |
| D、?x0>0,2 x0≥1 |
 某高校在2014年的自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩分组:第1组[75,80),第2组[80,85),第3组[85,90),第4组[90,95),第5组[95,100],得到的频率分布直方图如图所示.
某高校在2014年的自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩分组:第1组[75,80),第2组[80,85),第3组[85,90),第4组[90,95),第5组[95,100],得到的频率分布直方图如图所示.