题目内容

已知D、E、F分别是△ABC的边BC、CA、AB的中点，且
BC
=
a
，
CA
=
b
，
AB
=
c
，则①
EF
=
1
2
c
-
1
2
b
，②
BE
=
a
+
1
2
b
，③
CF
=-
1
2
a
+
1
2
b
，④
AD
+
BE
+
CF
=
0
中正确的等式的个数为
 
．
考点：向量加减混合运算及其几何意义
专题：平面向量及应用
分析：画出图形，结合图形，利用平面向量加减运算的几何意义进行解答即可．
解答： 解：如图所示，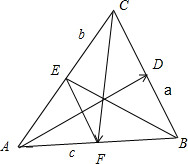
对于①，
EF
=
1
2
CB
=
1
2
（
CA
+
AB
）=
1
2
CA
+
1
2
AB
=
1
2
b
+
1
2
c
，∴①错误；
对于②，
BE
=
BC
+
CE
=
BC
+
1
2
CA
=
a
+
1
2
b
，∴②正确；
对于③，
CF
=
1
2
（
CB
+
CA
）=
1
2
CB
+
1
2
CA
=-
1
2
a
+
1
2
b
，∴③正确；
对于④，
AD
+
BE
+
CF
=
1
2
（
AC
+
AB
）+
1
2
（
BA
+
BC
）+
1
2
（
CA
+
CB
）
=
1
2
（
AC
+
AB
+
BA
+
BC
+
CA
+
CB
）=
0
，∴④正确；
综上，正确的等式个数是3．
故答案为：3．
点评：本题考查了平面向量的加减及数乘运算的应用问题，是基础题目．
练习册系列答案
相关题目
已知a=log34，b=log43，c=log53，则a，b，c的大小关系是（　　）
A、c＜a＜b
B、b＜a＜c
C、a＜c＜b
D、c＜b＜a
已知等差数列{an}中，a1007=4，S2014=2014，则S2015=（　　）
A、-2015B、2015
C、-4030D、4030
在平面直角坐标系xoy中，已知圆C1：（x+3）2+（y-1）2=4和圆C2：（x-4）2+（y-5）2=4．若直线l过点A（4，0），且被圆C1截得的弦长为2
3
，求直线l的方程．
A，B，C是△ABC的内角，向量
m
=（cos
3A
2
，sin
3A
2
），
n
=（cos
A
2
，sin
A
2
）满足|
m
+
n
|=
3

（1）求角A的大小
（2）若sinB+sinC=
3
sinA，试判断△ABC的形状．
在约束条件
x≥0
y≥0
x+y≤t
2x+y≤4
下，当3≤t≤4时，目标函数Z=3x+2y的最大值的变化范围是
 
．
以下有五个命题：
①若
a
∥
b
，
b
∥
c
，则
a
与
c
可能不平行；
②α，β都是第一象限角，且α＞β，则sinα＞sinβ；
③直线x=
π
4
是函数y=sinx+cosx图象的一条对称轴；
④在同一坐标系中，函数y=sinx的图象和函数y=x的图象只有一个公共点；
⑤对于y=3sin（2x+
π
4
），若f（x1）=f（x2）=0，则x1-x2是π的整数倍．
其中正确命题的序号是
 
．
阅读如图的程序框图，若输入m=2，n=3，则输出a=（　　）
A、6B、4C、3D、2
若做变速直线运动的物体v（t）=t2，在0≤t≤a内经过的路程为9，则a的值为
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网