题目内容
已知A,B,C,D,E为抛物线y=
x2上不同的五个点,焦点为F,且
+
+
+
+
=
,则|
|+|
|+|
|+|
|+|
|= .
| 1 |
| 4 |
| FA |
| FB |
| FC |
| FD |
| FE |
| 0 |
| FA |
| FB |
| FC |
| FD |
| FE |
考点:抛物线的简单性质
专题:圆锥曲线的定义、性质与方程
分析:
+
+
+
+
=
,可得xA-1+xB-1+xC-1+xD-1+xE-1=0,再利用焦点弦长公式即可得出.
| FA |
| FB |
| FC |
| FD |
| FE |
| 0 |
解答:
解:∵
+
+
+
+
=
,
∴xA-1+xB-1+xC-1+xD-1+xE-1=0,
则|
|+|
|+|
|+|
|+|
|=xA+xB+xC+xD+xE+
=5+5=10.
故答案为:10.
| FA |
| FB |
| FC |
| FD |
| FE |
| 0 |
∴xA-1+xB-1+xC-1+xD-1+xE-1=0,
则|
| FA |
| FB |
| FC |
| FD |
| FE |
| 5P |
| 2 |
故答案为:10.
点评:本题考查了抛物线的焦点弦长公式、向量运算,考查了计算能力,属于基础题.

练习册系列答案
相关题目
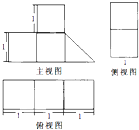
某几何体的三视图如图所示,则该几何体的体积为( )

A、
| ||
B、
| ||
C、
| ||
D、
|
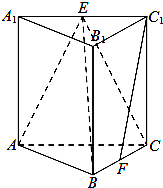 如图,在三棱柱ABC-A1B1C1中,CC1⊥平面ABC,A1B1⊥BC,BC=1,
如图,在三棱柱ABC-A1B1C1中,CC1⊥平面ABC,A1B1⊥BC,BC=1,