题目内容
若函数f(x)=sinx+cosx,f′(x)是f(x)的导函数,则函数F(x)=f(x)f′(x)+f2(x)的最大值 .
考点:利用导数求闭区间上函数的最值
专题:导数的概念及应用
分析:先对原函数求导数,然后再将F(x)表示出来,利用三角变换化成一个角、一种三角函数、一次的形式,再利用正弦函数的性质求最大值.
解答:
解:由已知得f′(x)=cosx-sinx,所以F(x)=f(x)f′(x)+f2(x)
=(cosx-sinx)(cosx+sinx)+(sinx+cosx)2.
=cos2x-sin2x+2sinxcosx+1
=cos2x+sin2x+1
=
sin(2x+
)+1.
因为sin(2x+
)≤1,
所以F(x)的最大值为1+
.
故答案为1+
.
=(cosx-sinx)(cosx+sinx)+(sinx+cosx)2.
=cos2x-sin2x+2sinxcosx+1
=cos2x+sin2x+1
=
| 2 |
| π |
| 4 |
因为sin(2x+
| π |
| 4 |
所以F(x)的最大值为1+
| 2 |
故答案为1+
| 2 |
点评:本题应先求出函数f(x)的导数,然后再得到F(x),将其化简成形如y=Asin(ωx+θ)的形式,再利用正弦函数的性质求解.

练习册系列答案
相关题目
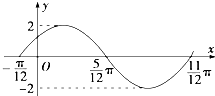 函数f(x)=Asin(ωx+ϕ)(A>0,ω>0,|φ|<
函数f(x)=Asin(ωx+ϕ)(A>0,ω>0,|φ|< 如图,正方体ABCD-A′B′C′D′的棱长为a.
如图,正方体ABCD-A′B′C′D′的棱长为a.