题目内容
条件p:
+1<0,条件q:|x+1|>2,则¬p是¬q的 条件(填充分不必要,必要不充分,充要条件)
| 1 |
| x-3 |
考点:必要条件、充分条件与充要条件的判断
专题:简易逻辑
分析:分别求出关于p,q的不等式,求出满足¬p,¬q的x的范围,结合充分必要条件的定义,从而得到答案.
解答:
解:解不等式
+1<0,得:2<x<3,
∴p:2<x<3,¬p:x≥3或x≤2,
解不等式|x+1|>2,得:x>1或x<-3,
∴q:x>1或x<-3,¬q:-3≤x≤1,
∴¬p是¬q的必要不充分条件,
故答案为:必要不充分.
| 1 |
| x-3 |
∴p:2<x<3,¬p:x≥3或x≤2,
解不等式|x+1|>2,得:x>1或x<-3,
∴q:x>1或x<-3,¬q:-3≤x≤1,
∴¬p是¬q的必要不充分条件,
故答案为:必要不充分.
点评:本题考查了充分必要条件,考查了解不等式问题,是一道基础题.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案
相关题目
若对任意一点O和不共线的三点A、B、C有
=x
+y
+z
,则x+y+z=1是四点P、A、B、C共面的( )
| OP |
| OA |
| OB |
| OC |
| A、必要不充分条件 |
| B、充分不必要条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
若f(x)是定义在R上的增函数,则对任意x、y∈R,“f(x)+f(y)<f(-x)+f(-y)”是“x+y<0”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、既不充分又不必要条件 |
设扇形的弧长为2,面积为2,则扇形中心角的弧度数是( )
| A、1 | B、4 | C、1或4 | D、π |
命题“如果x>0,那么x+
≥2”的逆否命题是( )
| 1 |
| x |
A、如果x≤0,那么x+
| ||
B、如果x+
| ||
C、如果x+
| ||
D、如果x>0,那么x+
|
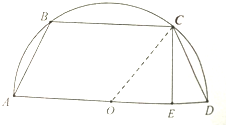 在半径为1的半圆中,作如图所示的等腰梯形ABCD,CE垂直下底AD于E,设DE=x(0<x<1),CE=h,梯形ABCD的周长为L.
在半径为1的半圆中,作如图所示的等腰梯形ABCD,CE垂直下底AD于E,设DE=x(0<x<1),CE=h,梯形ABCD的周长为L.