题目内容
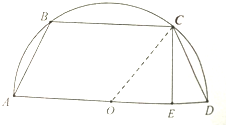在半径为1的半圆中，作如图所示的等腰梯形ABCD，CE垂直下底AD于E，设DE=x（0＜x＜1），CE=h，梯形ABCD的周长为L．（1）求h关于x的函数解析式，并指出定义域；
（2）试写出L与关于x的函数解析式，并求周长L的最大值．
考点：函数解析式的求解及常用方法
专题：函数的性质及应用
分析：（1）根据图形，便有h=
=
，并且定义域为（0，1）；
（2）容易求出|CD|=
，|BC|=2-2x，所以周长L=-2x+2
+4，对该函数解析式配方即可求出周长L的最大值．
| 1-(1-x)2 |
| -x2+2x |
（2）容易求出|CD|=
| 2x |
| 2x |
解答：
解：（1）h2=1-（1-x）2=-x2+2x；
∴h=
，定义域为（0，1）；
（2）如图，|CD|=
=
；
|BC|=2-2x；
∴L=2
+2-2x+2=2
-2x+4=-2(
-
)2+5，x∈（0，1）；
即L=-2(
-
)2+5，x∈（0，1）；
∴
=
，即x=
时，L取最大值5．
∴h=
| -x2+2x |
（2）如图，|CD|=
| h2+x2 |
| 2x |
|BC|=2-2x；
∴L=2
| 2x |
| 2x |
| x |
| ||
| 2 |
即L=-2(
| x |
| ||
| 2 |
∴
| x |
| ||
| 2 |
| 1 |
| 2 |
点评：考查根据实际问题求函数解析式的方法，直角三角形边的关系，梯形周长的概念，以及配方求函数最大值的方法．
练习册系列答案
相关题目
如图，已知AB是半圆O的直径，AB=8，M，N，P是将半圆圆周四等分的三个分点，从A，B，M，N，P这5个点中任取3个点，则这3个点组成直角三角形的概率为（ ）A、
| ||
B、
| ||
C、
| ||
D、
|
在△ABC中，a，b，c分别是角A，B，C的对边，且满足acosA=bcosB，那么△ABC的形状一定是 （ ）
| A、等腰三角形 |
| B、直角三角形 |
| C、等腰或直角三角形 |
| D、等腰直角三角形 |