题目内容
已知
=2,则tan(x+
)的值为 ( )
sin(
| ||
| cos(-x)+sin(2π-x) |
| 3π |
| 4 |
| A、2 | ||
| B、-2 | ||
C、
| ||
D、-
|
考点:两角和与差的正切函数,运用诱导公式化简求值
专题:三角函数的求值
分析:直接利用诱导公式化简已知条件,求出正切函数值,利用两角和与差的正切函数求解即可.
解答:
解:已知
=2,
即
=2,
∴tanx=
.
tan(x+
)=
=
=-
.
故选:D.
sin(
| ||
| cos(-x)+sin(2π-x) |
即
| cosx+sinx |
| cosx-sinx |
∴tanx=
| 1 |
| 3 |
tan(x+
| 3π |
| 4 |
tanx+tan
| ||
1-tanxtan
|
| ||
1+
|
| 1 |
| 2 |
故选:D.
点评:本题考查两角和与差的三角函数,诱导公式的应用,基本知识的考查.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
函数y=
(a<0且a为常数)在区间(-∞,1]上有意义,则实数a的取值范围( )
| ax+1 |
| A、[-1,0) |
| B、(-1,0) |
| C、[-1,0] |
| D、(-1,+∞) |
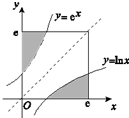 如图,由x=0,x=e,y=0,y=e,y=lnx,y=ex六条曲线共同围成的面积为
如图,由x=0,x=e,y=0,y=e,y=lnx,y=ex六条曲线共同围成的面积为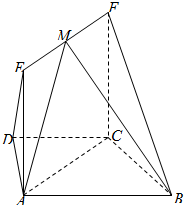 如图,在梯形ABCD中,AB∥CD,AD=DC=CB=2,∠CBA=30°,四边形ACFE为矩形,平面ACFE⊥平面ABCD,CF=3.
如图,在梯形ABCD中,AB∥CD,AD=DC=CB=2,∠CBA=30°,四边形ACFE为矩形,平面ACFE⊥平面ABCD,CF=3.