题目内容
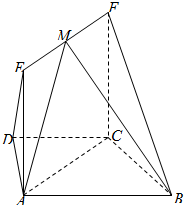 如图,在梯形ABCD中,AB∥CD,AD=DC=CB=2,∠CBA=30°,四边形ACFE为矩形,平面ACFE⊥平面ABCD,CF=3.
如图,在梯形ABCD中,AB∥CD,AD=DC=CB=2,∠CBA=30°,四边形ACFE为矩形,平面ACFE⊥平面ABCD,CF=3.(1)求证:BC⊥平面ACFE;
(2)设点M为EF中点,求二面角B-AM-C的余弦值.
考点:二面角的平面角及求法,直线与平面垂直的判定
专题:空间位置关系与距离,空间角
分析:(1)由已知得BC⊥AC,由此能证明BC⊥平面ACEF.
(II)过C作CH⊥AM,交AN于点H,连BH,从而∠CHB为二面角B-AM-C的平面角,由此能求出二面角B-AM-C的余弦值.
(II)过C作CH⊥AM,交AN于点H,连BH,从而∠CHB为二面角B-AM-C的平面角,由此能求出二面角B-AM-C的余弦值.
解答:
(本小题满分14分)
(1)证明:∵AD=DC=CB=2,∠ABC=60°,
则AB=4,AC2=12,则得AB2=AC2+BC2,
∴BC⊥AC,∵面ACEF⊥平面ABCD,
面ACEF∩平面ABCD=AC,
∴BC⊥平面ACEF.(7分)
(II)解:过C作CH⊥AM,交AN于点H,连BH,
∵BC⊥平面ACFE,∴BC⊥AM,而AM⊥CH,∴AM⊥平面BCD,∴BH⊥AM,
则∠CHB为二面角B-AM-C的平面角,
在Rt△BHC中,CH=3,HB=
,cos∠CHB=
,
则二面角B-AM-C的余弦值为
.(14分)
(1)证明:∵AD=DC=CB=2,∠ABC=60°,
则AB=4,AC2=12,则得AB2=AC2+BC2,
∴BC⊥AC,∵面ACEF⊥平面ABCD,
面ACEF∩平面ABCD=AC,
∴BC⊥平面ACEF.(7分)
(II)解:过C作CH⊥AM,交AN于点H,连BH,
∵BC⊥平面ACFE,∴BC⊥AM,而AM⊥CH,∴AM⊥平面BCD,∴BH⊥AM,
则∠CHB为二面角B-AM-C的平面角,
在Rt△BHC中,CH=3,HB=
| 13 |
3
| ||
| 13 |
则二面角B-AM-C的余弦值为
3
| ||
| 13 |
点评:本题考查直线与平面垂直的证明,考查二面角的余弦值的求法,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
相关题目
如图,向量
-
等于 ( )

| a |
| b |

A、-2
| ||||
B、-4
| ||||
C、
| ||||
D、-
|
已知
=2,则tan(x+
)的值为 ( )
sin(
| ||
| cos(-x)+sin(2π-x) |
| 3π |
| 4 |
| A、2 | ||
| B、-2 | ||
C、
| ||
D、-
|
双曲线
-
=1(b>0)的一条渐近线方程为y=
x,则双曲线的离心率等于( )
| x2 |
| 9 |
| y2 |
| b2 |
| 2 |
| 3 |
A、
| ||||
B、
| ||||
| C、C、 | ||||
D、
|
