题目内容
18. 如图,已知正四棱柱(底面为正方形,侧棱与底面垂直)ABCD-A1B1C1D1的底面边长为3,侧棱长为4,连结A1B,过A作AF⊥A1B垂足为F,且AF的延长线交B1B于E.
如图,已知正四棱柱(底面为正方形,侧棱与底面垂直)ABCD-A1B1C1D1的底面边长为3,侧棱长为4,连结A1B,过A作AF⊥A1B垂足为F,且AF的延长线交B1B于E.(Ⅰ)求证:AE⊥D1B;
(Ⅱ)求三棱锥B-AEC的体积.
分析 (Ⅰ)推导出A1D1⊥AE,AE⊥A1B,从而AE⊥平面A1D1B,由此能证明AE⊥D1B.
(Ⅱ)以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系,三棱锥B-AEC的体积VB-AEC=VE-ABC,由此能求出结果.
解答 证明:(Ⅰ)∵正四棱柱(底面为正方形,侧棱与底面垂直)
ABCD-A1B1C1D1中,A1D1⊥平面ABB1A1,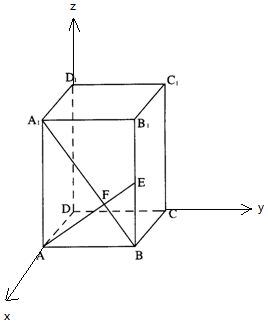
AE?平面ABB1A1,
∴A1D1⊥AE,
∵过A作AF⊥A1B垂足为F,且AF的延长线交B1B于E,∴AE⊥A1B,
∵A1D1∩A1B=A1,∴AE⊥平面A1D1B,
∵D1B?平面A1D1B,∴AE⊥D1B.
解:(Ⅱ)以D为原点,DA为x轴,DC为y轴,
DD1为z轴,建立空间直角坐标系,
则A(3,0,0),B(3,3,0),A1(3,0,4),
设E(3,3,t),
$\overrightarrow{AE}$=(0,3,t),$\overrightarrow{{A}_{1}B}$=(0,3,-4),
∵AE⊥A1B,∴$\overrightarrow{AE}•\overrightarrow{{A}_{1}B}$=9-4t=0,解得t=$\frac{9}{4}$,
∴BE=$\frac{9}{4}$,
∴三棱锥B-AEC的体积:
VB-AEC=VE-ABC=$\frac{1}{3}×BE×{S}_{△ABC}$=$\frac{1}{3}×BE×(\frac{1}{2}×AB×BC)$
=$\frac{1}{3}×\frac{9}{4}×\frac{1}{2}×3×3$=$\frac{27}{8}$.
点评 本题考查线线垂直的证明,考查三棱锥的体积的求法,考查空间中线线、线面、面面间的位置关系,考查推理论证能力、运算求解能力,考查化归与转化思想、函数与方程思想,是中档题.

| A. | 若a>b,c>d,则ac>bd | B. | 若ac>bc,则a>b | ||
| C. | 若a>b,c>d,则a-c>b-d | D. | 若$\frac{a}{{c}^{2}}$<$\frac{b}{{c}^{2}}$,则a<b |
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
| A. | 科学家利用鱼的沉浮原理制造潜艇 | |
| B. | 猜想数列$\frac{1}{1×2}$,$\frac{1}{2×3}$,$\frac{1}{3×4}$,…的通项公式为an=$\frac{1}{n(n+1)}$(n∈N+) | |
| C. | 半径为r的圆的面积S=πr2,则单位圆的面积S=π | |
| D. | 由平面直角坐标系中圆的方程为(x-a)2+(y-b)2=r2,推测空间直角坐标系中球的方程为(x-a)2+(y-b)2+(z-c)2=r2 |
| A. | (-$\frac{1}{2}$,1] | B. | (-$\frac{1}{2}$,1) | C. | (-$\frac{1}{2}$,$\frac{1}{2}$) | D. | (-$\frac{1}{2}$,$\frac{1}{2}$] |