题目内容
14.若直线ax+y-2=0与圆心为C的圆(x-1)2+(y-a)2=16相交于A,B两点,且$\overrightarrow{CA}•\overrightarrow{CB}=0$,则实数a的值是-1.分析 由向量垂直的条件:数量积为0,结合圆的知识可得△ABC为等腰直角三角形,求出圆的圆心和半径,弦长AB,以及圆心到直线的距离,运用点到直线的距离公式,解方程即可得到a的值.
解答 解:由题意$\overrightarrow{CA}•\overrightarrow{CB}=0$,
结合圆的知识可得△ABC为等腰直角三角形,
圆(x-1)2+(y-a)2=16的圆心C(1,a),半径r=4,
弦长AB=4$\sqrt{2}$,
由等腰直角三角形的性质可得C到直线的距离为d=2$\sqrt{2}$,
即有$\frac{|a+a-2|}{\sqrt{{a}^{2}+1}}$=2$\sqrt{2}$,
解得a=-1.
故答案为:-1.
点评 本题考查直线和圆相交的弦长求法和向量垂直的条件:数量积为0,考查等腰直角三角形的性质,以及点到直线的距离公式的运用,考查运算能力,属于中档题.

练习册系列答案
相关题目
4.已知$cos(3π-α)=\frac{4}{5}$,则cos(π+α)的值是( )
| A. | $\frac{4}{5}$ | B. | -$\frac{4}{5}$ | C. | $\frac{3}{5}$ | D. | -$\frac{3}{5}$ |
5.假设你和同桌玩数字游戏,两人各自在心中想一个整数,分别记为x,y,且x,y∈[1,4].如果满足|x-y|≤1,那么就称你和同桌“心灵感应”,则你和同桌“心灵感应”的概率为( )
| A. | $\frac{7}{16}$ | B. | $\frac{5}{8}$ | C. | $\frac{9}{16}$ | D. | $\frac{7}{8}$ |
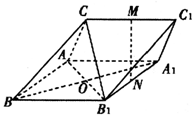 如图,三棱柱ABC-A1B1Cl中,M,N分别为CC1,A1B1的中点.CA⊥CB1,CA=CB1,BA=BC=BB1.
如图,三棱柱ABC-A1B1Cl中,M,N分别为CC1,A1B1的中点.CA⊥CB1,CA=CB1,BA=BC=BB1. 如图,已知正四棱柱(底面为正方形,侧棱与底面垂直)ABCD-A1B1C1D1的底面边长为3,侧棱长为4,连结A1B,过A作AF⊥A1B垂足为F,且AF的延长线交B1B于E.
如图,已知正四棱柱(底面为正方形,侧棱与底面垂直)ABCD-A1B1C1D1的底面边长为3,侧棱长为4,连结A1B,过A作AF⊥A1B垂足为F,且AF的延长线交B1B于E.